1- Tipos de ángulos según su posición
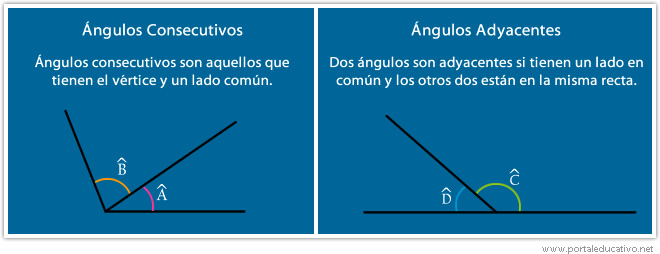
– Ángulos consecutivos
– Ángulos adyacentes
– Ángulos opuestos por el vértice
En resumen:
Los ángulos consecutivos tienen en común un vértice y un lado.
Los ángulos adyacentes son ángulos consecutivos que tienen los lados no comunes en la misma recta.
Nota: Los ángulos adyacentes son suplementarios.
–
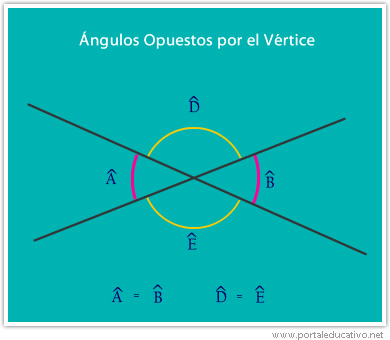
Ángulos opuestos por el vértice
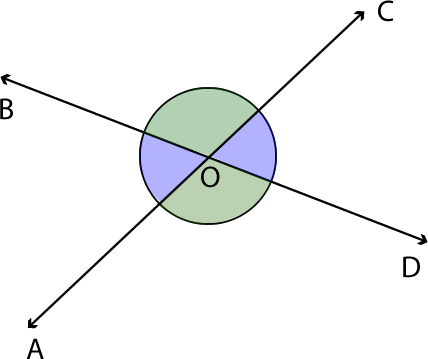
En la siguiente imagen se muestran dos rectas que se cortan, ¿qué relaciones hay entre los ángulos del mismo color?
Al medir los ángulos de color azul con el transportador, puedes determinar que ambos tienen la misma medida.
¿Los ángulos de color verde también tienen la misma medida?
Si medimos con un trasportador la medida de estos ángulos, podemos comprobar que tienen la misma medida. En este caso, los ángulos del mismo color son opuestos por el vértice.

Como puedes ver, dos rectas que se cortan determinan dos parejas de ángulos opuestos por el vértice.
Los ángulos opuestos por el vértice tienen el vértice en común y las prolongaciones de los lados de uno de ellos corresponden a los lados del otro. Los ángulos opuestos por el vértice miden lo mismo.
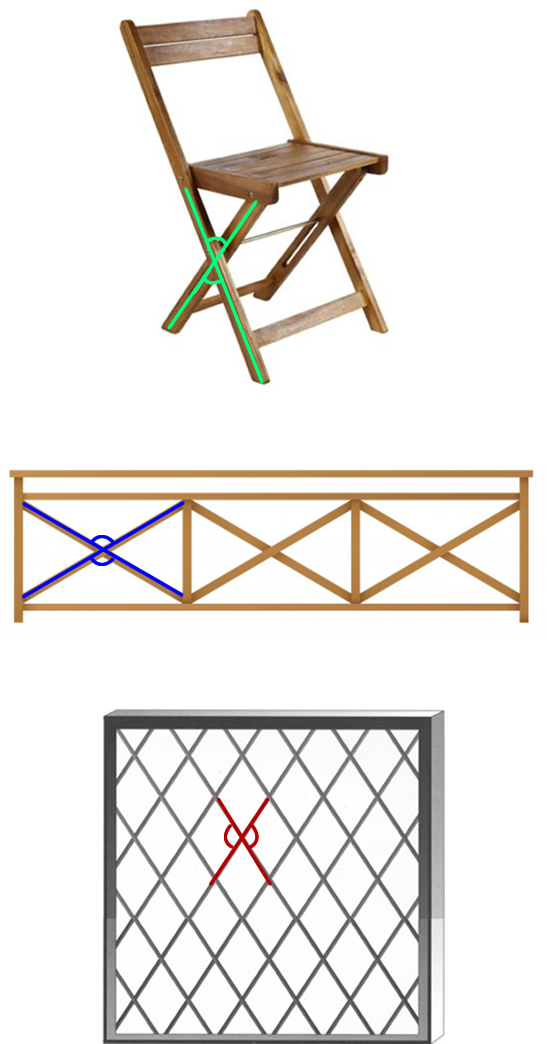
¿Dónde están presentes este tipo de ángulos en la vida cotidiana?
Por ejemplo en una silla plegable, un cerco o una reja.
2- Clases de ángulos según su suma
Según la suma de sus medidas dos ángulos pueden ser :
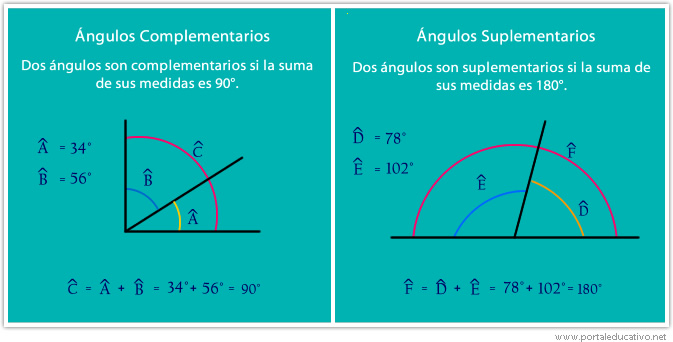
– Ángulos complementarios
– Ángulos suplementarios
Ejemplos:
El complemento de un ángulo de 28° es un ángulo de 62°. Ya que 28° + 62° = 90°
El complemento de un ángulo 40° es un ángulo de 50°. Ya que 40° + 50° = 90°
El suplemento de un ángulo de 18° es un ángulo de 162°. Ya que 18° + 162° = 180°
El suplemento de un ángulo de 136° es un ángulo de 44°. Ya que 136° + 44° = 180°
En resumen:
– Dos ángulos son complementarios si su suma es igual a 90°.
– Dos ángulos son suplementarios si su suma es igual a 180°.
Reflexiona, ¿dónde se pueden apreciar este tipo de ángulos en la vida cotidiana?
– El truco está en acordarse que para calcular el ángulo complementario de uno o unos ángulos dados deberemos restarle a 90° su amplitud/es y para calcular el ángulo suplementario, habrá que restarle a 180° su amplitud/es.
3- Ángulos entre paralelas y una recta transversal
Las rectas paralelas las podemos ver en la vida cotidiana de diversas formas: construcciones, escaleras, planos, diseños de pisos, cables del tendido eléctrico, entre otras.
En este caso, la baranda de la escalera está formado por barras metálicas paralelas entre sí y por otras que las intersectan.
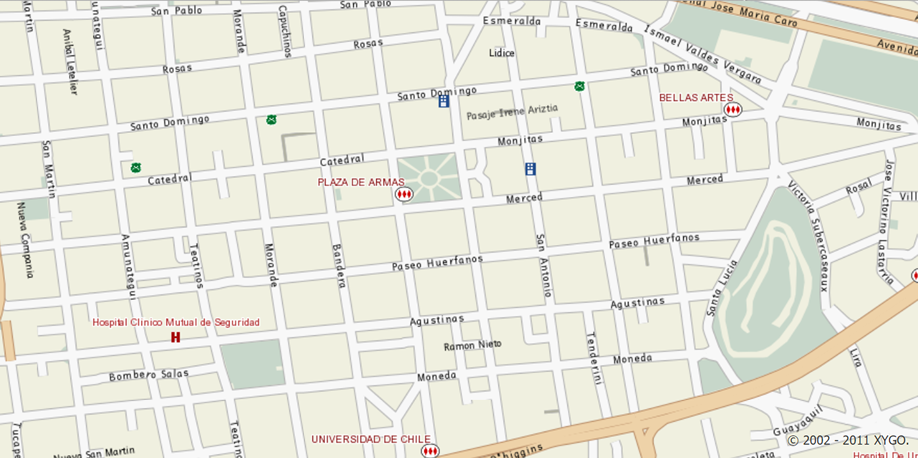
En el plano se pueden apreciar calles que son paralelas y que son intersectadas por otras.
Fuente: http://mapas.emol.com/
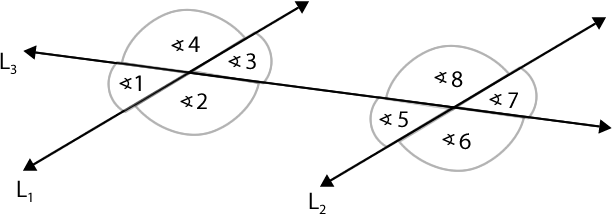
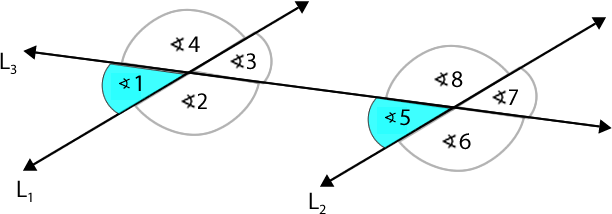
Al trazar dos rectas paralelas cortadas por una transversal, se forman 8 ángulos como se aprecia en la imagen:
¿Qué relaciones se pueden establecer entre estos ángulos?
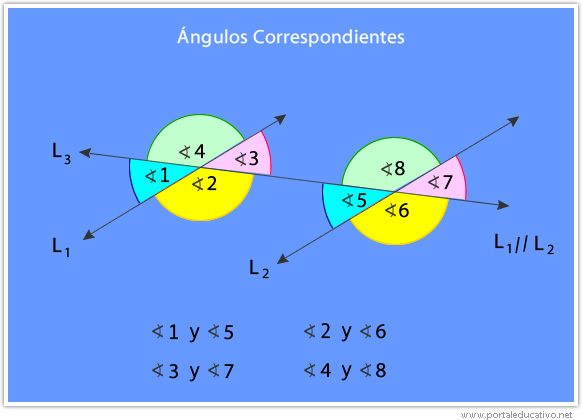
3.1- Ángulos correspondientes:
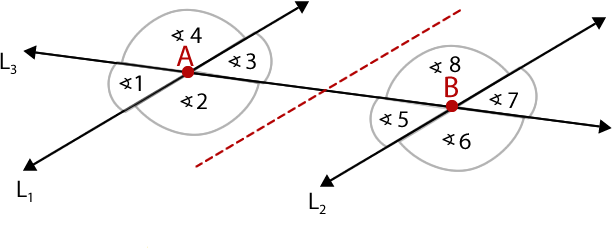
Imagina que recortas la figura por la línea segmentada. Luego haces calzar los vértices A y B.
Podrás darte cuenta de que hay pares de ángulos que son iguales.
Al aplicar una traslación, el ángulo 1 queda en la posición del ángulo 5, por lo tanto, tienen las mismas medidas.
Algo similar ocurre con los ángulos 2, 3 y 4, ya que quedan en la posición de los ángulos 6, 7 y 8 respectivamente. Estos tipos de ángulos son correspondientes.
Los ángulos correspondientes son aquellos que ocupan la misma posición relativa con respecto a la recta transversal. Los ángulos correspondientes tienen igual medida.
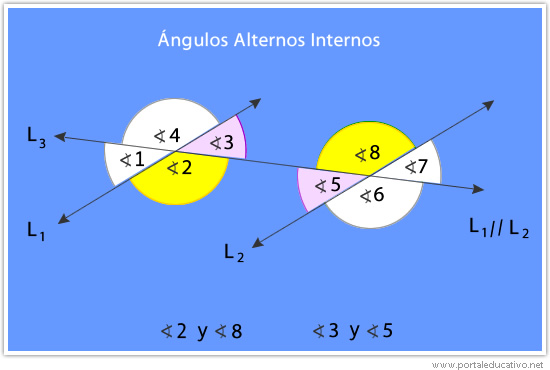
3.2- Ángulos alternos internos: Son aquellos que se encuentran al interior de la región generada por las rectas paralelas y a lados opuestos de la recta transversal. Los ángulos alternos internos tienen igual medida.
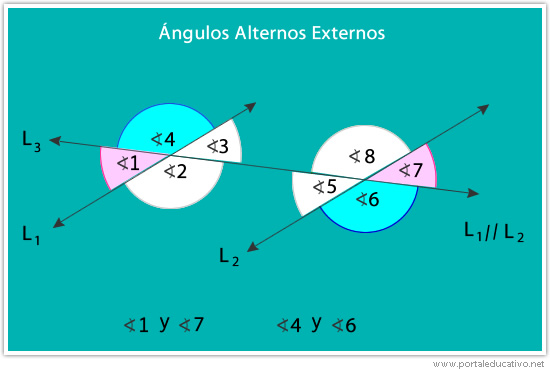
3.3- Ángulos alternos externos: Son aquellos que no son consecutivos y que se encuentran fuera de la región entre las rectas paralelas y a lados opuestos de la recta transversal. Los ángulos alternos externos tienen igual medida.
También podemos distinguir ángulos opuestos por el vértice y suplementarios.
Por ejemplo los ángulos 4 y 2 son opuestos por el vértice y los ángulos 5 y 8 son suplementarios, ¿qué otros ángulos opuestos por el vértice puedes identificar?, ¿y suplementarios?
4- Ejercicios resueltos
4.1- En la imagen, m( 1) es 50°, determina la medida de los siguientes ángulos considerando que L1 // L2:
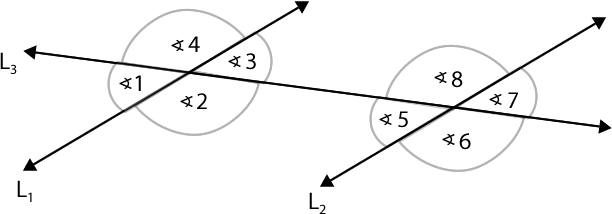
a) m( 3)
b) m( 4)
c) m( 5)
d) m( 7)
e) m( 8)
Desarrollo:
a) m( 3)
El 1 y el 3 son opuestos por el vértice, entonces tiene la misma medida.
m( 3) = 50°.
b) m( 4)
El 1 y el 4 son suplementarios, por lo que suman 180°.
Para determinar la medida del 4 se resta 180 – 50 = 130°
m( 4) = 130°.
c) m( 5)
El 1 y el 5 son correspondientes, por lo tanto, tienen la misma medida.
m( 5) = 50°.
d) m( 7)
El 1 y el 7 son alternos externos, por lo que tienen la misma medida.
m( 7) = 50°.
e) m( 8)
El 4 y el 8 son correspondientes, entonces miden lo mismo.
m( 8)= 130°.
4.2- En la imagen se muestra el paralelogramo ABCD. Calcula la medida de sus ángulos interiores considerando que el CBA mide 115°.
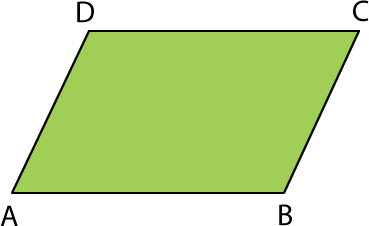
Los lados AB y DC son paralelos, al igual que AD y BC. Al prolongar sus lados, se pueden identificar ángulos opuestos por el vértice. Además, se pueden reconocer ángulos correspondientes y suplementarios.
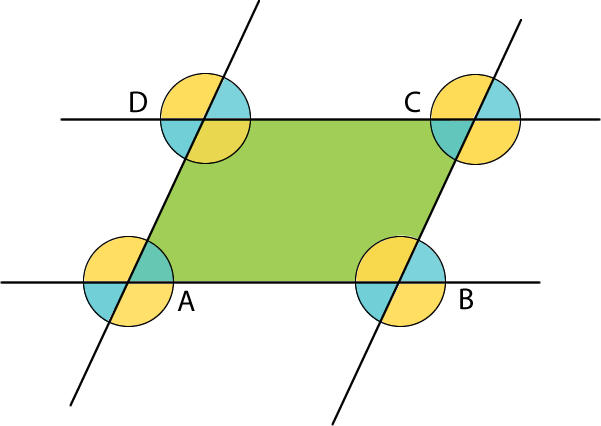
A continuación, calculamos el suplemento de 115°. Este corresponde a 65°, porque 115° + 65° = 180°.
Entonces los ángulos de color celeste miden 65° y los de color amarillo miden 115°.
Por último, determinamos las medidas de los ángulos interiores del paralelogramo:
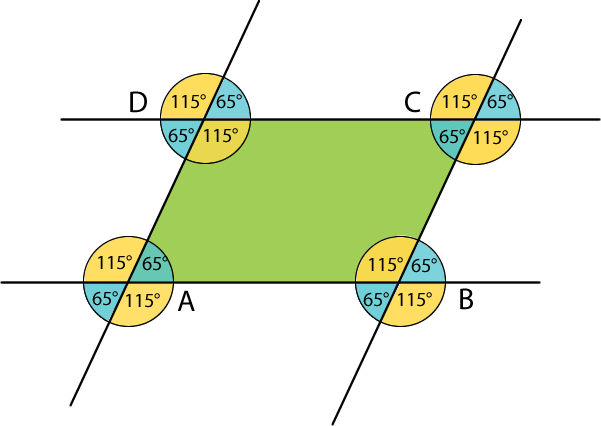
m(CBA)= 115°
m(BAD)= 65°
m(ADC)= 115°
m(DCB)= 65°