1- Proporción
Recordemos: Una proporción es la igualdad de dos razones.
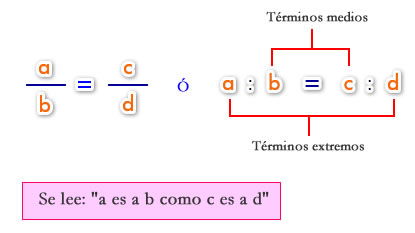
1.1- Propiedad fundamental
En toda proporción, el producto de los términos medios es igual al producto de los términos extremos (Teorema fundamental de las proporciones). Es decir:

Ejemplo: Si tenemos la proporción:
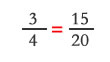
y le aplicamos la propiedad fundamental señalada queda: 3 • 20 = 4 • 15, es decir, 60 = 60.
Esta es la propiedad que nos permite detectar si dos cantidades presentadas como proporción lo son verdaderamente.
2- Proporcionalidad directa
Dos variables (una independiente x y la otra dependiente y ) son directamente proporcionales si el cociente (división) entre los valores respectivos de cada una de las variables es constante.
y / x = k
Además al aumentar o disminuir una de ellas, la otra aumenta o disminuye, respectivamente, en la misma razón.
Ejemplo:
– Indica si las variables son directamente proporcionales
a. La medida del lado de un cudrado y su perímetro:
Respuesta Sí, porque a mayor longitud de sus lados mayor perímetro (si una variable aumenta, la otra aumenta en la misma razón).
b. El número de trabajadores y los días que se demoran en hacer un trabajo, si todos trabajan de igual manera: Respuesta: No, porque a mayor cantidad de trabajadores menos cantidad de días. (si una variable aumenta, la otra disminuye en la misma razón).
En el caso de las funciones esta proporcionalidad directa se puede representar como una función de la forma
y = k x
Donde:
y : variable dependiente.
x: variable independiente.
k : constante de proporcionalidad.
Por ejemplo: si tenemos la siguiente función:
y = 3 x
La constante de proporcionalidad sería 3.
2.1- ¿Cómo se calcula la constante de proporcionalidad?
Como y = k x entonces: k = y / x
Calcula la constante de proporcionalidad:
| x | 3 | 6 | 7 |
| y | 6 | 12 | 14 |
k = 6 / 3
k = 2
El cociente de las dos magnitudes es siempre el mismo (constante)
2.2- Gráfico de proporcionalidad directa
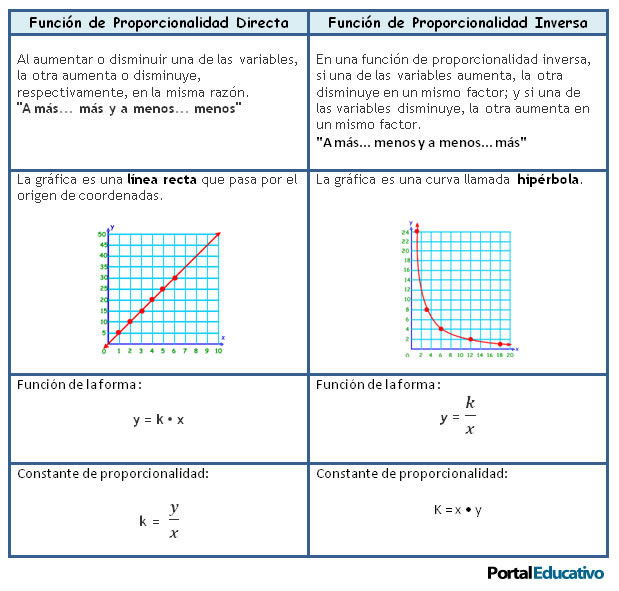
El gráfico correspondiente a una relación de proporcionalidad directa es una línea recta que pasa por el punto de origen de un sistema de coordenadas cartesianas.
En una función de proporcionalidad directa, si una de las variables aumenta, la otra también aumenta en un mismo factor; y si una de las variables disminuye, la otra disminuye en un mismo factor.
Ejemplo:
Juan ha utilizado 20 huevos para hacer 4 tortillas iguales. ¿Cuántos huevos necesita para hacer 6 tortillas? ¿Y para hacer 2?
Grafica los resultados hasta 6 tortillas.
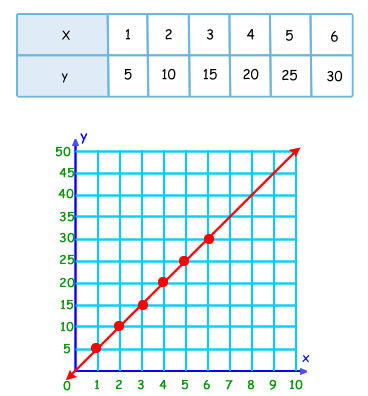
Como puedes ver, el gráfico es una línea recta que pasa por el origen. Además si nos fijamos en la tabla, nos podemos dar cuenta que el cociente (división) entre las dos magnitudes (y / x) es constante. En este caso el valor de la constante de proporcionalidad es 5.
3- Proporcionalidad inversa
Dos variables (una independiente x y la otra dependiente y ) son inversamente proporcionales si el producto entre los valores respectivos de cada una de las variables es constante.
( x • y = k )
Además, en una función de proporcionalidad inversa, si una de las variables aumenta, la otra disminuye en un mismo factor; y si una de las variables disminuye, la otra aumenta en un mismo factor.
Esta relación de proporcionalidad inversa se puede representar como una función de la forma:
y = k / x
Donde:
y : variable dependiente.
x: variable independiente.
k : constante de proporcionalidad.
Ejemplos:
3.1- Gráfico de proporcionalidad inversa
La representación gráfica de esta función son puntos que pertenecen a una curva, llamada hipérbola.
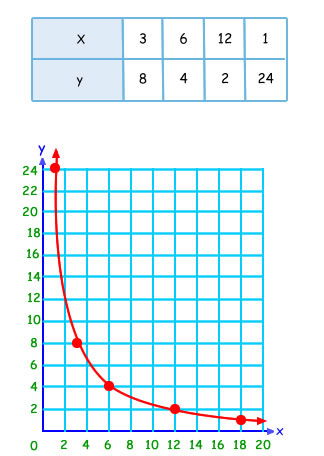
Resumen: Observa el siguiente cuadro comparativo: