1- ¿Qué es la trigonometría?
La trigonometría corresponde a un área de la matemática dedicada, en sus inicios, al estudio de los elementos de los triángulos para lo cual se dedica a estudiar la relación entre sus ángulos y sus lados.
Para medir ángulos existen tres unidades de medida:
– El radián (1 rad), es el ángulo central de una circunferencia que abarca un arco con igual longitud que el radio.

– El grado sexagesimal (°), que se obtiene al dividir una circunferencia en 360 partes iguales. Sus subunidades de medida son los minutos y segundos.
– El grado centesimal o gradián (°C), corresponde a cada una de las porciones que se obtienen al dividir la circunferencia en cuatrocientos gradianes.
¿Cómo se relacionan?
Para convertir de una unidad a otra, debemos considerar que un ángulo extendido equivale a:

Aplicando proporción directa (regla de tres simple)
a) Para convertir 45 gradianes a sexagesimal:
45°C → x°
200°C → 180°
Luego: x° = (45 • 180) / 200 = 40,5°
b) Para convertir 40,5° a radianes:

Otras equivalencias:
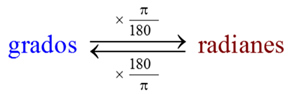
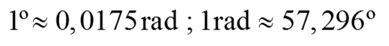
¿Cómo lo realizo con la calculadora?
Simplemente cambiando el modo. Pulsa”Mode” hasta que aparezca:

Luego, selecciona la unidad de medida de ángulo que necesites usar.
¿Cuándo las uso?
Nuestro sistema de medición corresponde al grado sexagesimal, es común mencionar que un ángulo mide 45° ó 60°. Sin embargo, en trigonometría es muy común utilizar los radianes.
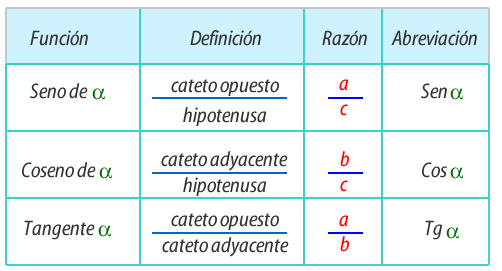
2- Razones trigonométricas
Las razones trigonométricas relacionan la medida de un ángulo con los lados de un triángulo. Para ello se basan en el triángulo rectángulo, donde encontramos dos ángulos agudos y complementarios (suman 90°) y sus lados reciben el nombre de catetos e hipotenusa.
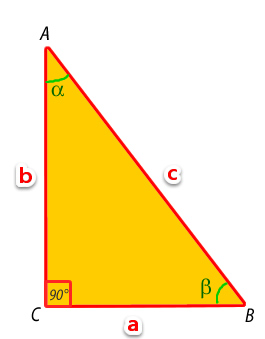
Δ ABC rectángulo en C. a y b son catetos, c es la hipotenusa, α y β son ángulos agudos.Cada ángulo agudo tiene un cateto opuesto y un cateto adyacente.
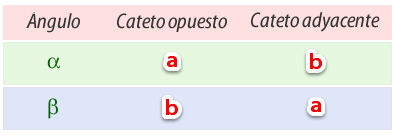
Así, se definen las razones trigonométricas de un ángulo como la razón entre las medidas de los lados de un triángulo.
Para resolver un problema de aplicación, debemos considerar que con los datos que este nos entrega:
– podamos formar un triángulo rectángulo
– tener presente la posición del ángulo y los lados.
Por ejemplo:
a) Un árbol forma una sombra 12 m largo. El ángulo a la parte superior del árbol desde el final de la sombra es 68°. Encuentre la altura del árbol.
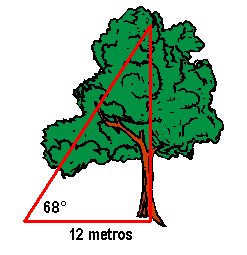
El árbol mide 29,7 m aproximadamente.
Recordar que podemos conocer el valor de tg 68 mediante el uso de la calculadora, que es aproximadamente 2,475
2) Marta y Rafael caminan por la avenida separados 100 m. Marta ve la esquina izquierda de la azotea de un edificio con un ángulo de elevación de 40º, y Rafael lo hace con un ángulo de 70º. Hallar su altura.
El problema nos plantea esta situación:
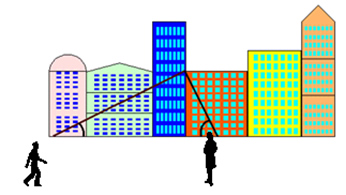
Si formamos el triángulo resulta:
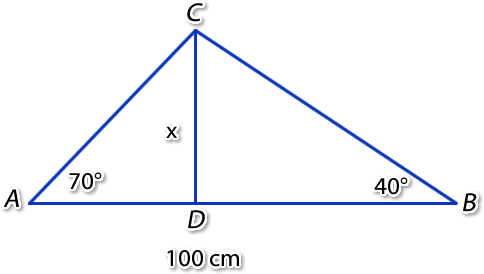
AD + DB = 100 ⇒ AD = 100 – DB
Los lados dados, corresponden a catetos del Δ ADC y Δ BDC, rectángulos en D. Por lo tanto, podemos calcular tangentes de los ángulos dados:
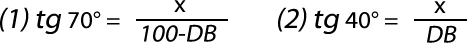
tg 70 ≈ 2,747 tg 40 ≈ 0,83909
Despejamos DB en (2) y lo reemplazamos en (1), resultando:

3- Razones trigonométricas de ángulos especiales
Se llaman “ángulos especiales” a los ángulos de 30°, 45° y 60° ya que son ángulos interiores que se encuentran en un triángulo equilátero e isósceles rectángulo. Con estos triángulos, podemos analizar de manera mucho más efectiva la trigonometría.
Observa:
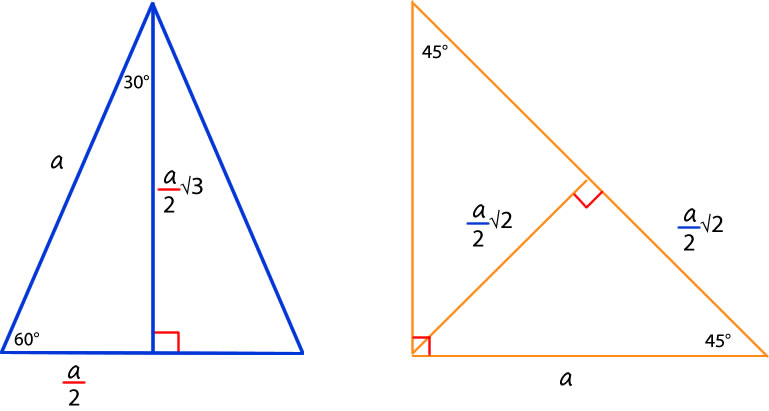
A partir de esto, podemos examinar la siguiente tabla:

En resumen:
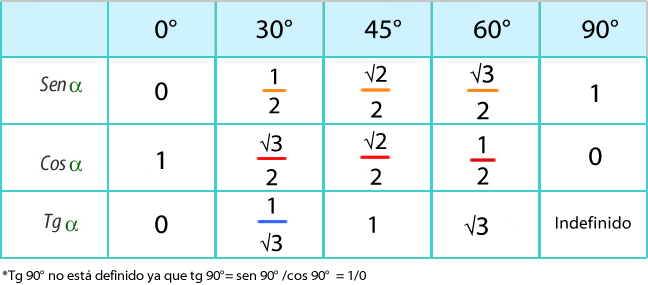
Consejos para aprenderse las fórmulas
(1) El seno y el coseno de los ángulos estudiados pueden escribirse como un patrón de raices, lo cual facilita la memorización de las formulas.
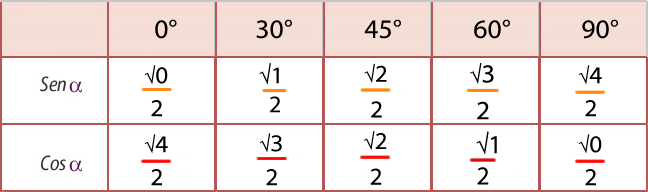
(2) Mientras el seno va aumentando su valor, el coseno va disminuyendo.
(3) Hay algunas equivalencias dentro de los ángulos estudiados. Podría decirse que son equivalencias "espejo", ya que una se repite con la que está a la misma distancia en la tabla.
Cos 0 = Sen 90
Cos 30 = Sen 60
Cos 45 = Sen 45
Cos 60 = Sen 30
Cos 90 = Sen 0
(4) La tangente tambien se puede memorizar facil. Lo que debes hacer es recordar de memoria Tg 30 (1/√3). Luego, en el ángulo que viene (45) debes anotar lo que hay en el numerador de Tg 30 (1) y luego, en el próximo (60) debes anotar lo que está en el denominador (√3).
EJERCITA
Calcula la altura, h, de los siguientes triángulos:
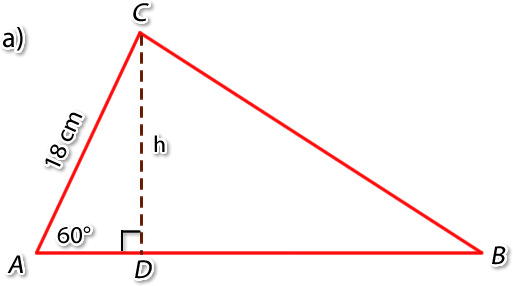
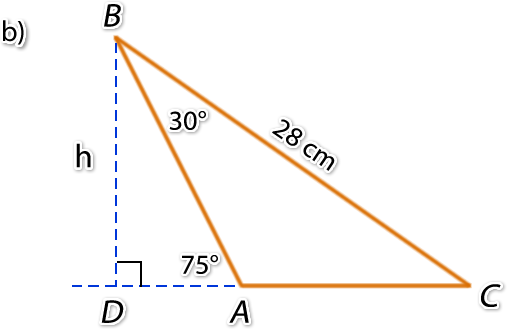
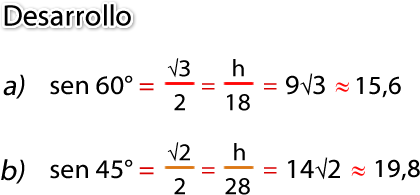
*Se llega a sen 45 encontrando los ángulos internos que faltan, mediante la regla de que la suma de los ángulos interiores de un triángulo es 180 grados.
4.- Ángulo de elevación y de depresión
Son aquellos formandos por la horizontal (considerada a nivel del ojo del observador) y la línea de mira. El grado del ángulo dependerá del objetivo observado.

Con respecto a un observador, los ángulos de elevación y de depresión constituyen ángulos alternos internos entre paralela, por lo tanto, sus medidas son iguales.
Por ejemplo:
Desde la parte alta de una torre de 120m de altura, el ángulo de depresión de un objeto colocado en el plano horizontal de la base de la torre es de 24°. ¿Qué tan lejos está el objeto del pie de la torre? ¿A qué distancia del observador está el objeto?
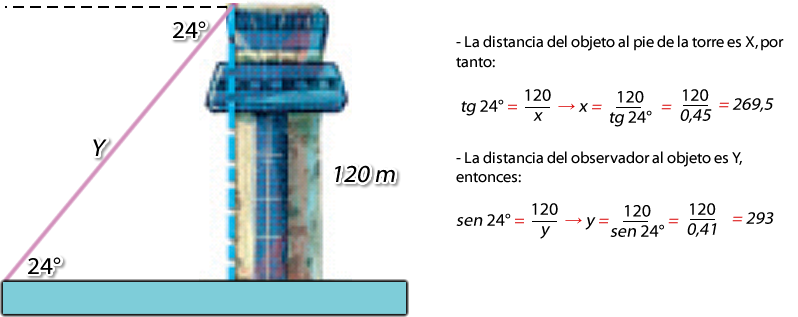
El objeto está a 270 metros, aprox., del pie de la torre. Y, a 293 metros, aprox., del observador.
Ejercicios
1) Una escalera de 12 metros llega hasta la parte superior de un muro. Si la escalera forma un ángulo de 36° con el muro. Encontrar la altura del muro.
La altura del muro es 9.71 m
2) Un cable está sujeto a lo alto de una antena de radio y a un punto en el suelo horizontal que está a 40m de la base de la antena. Si el cable forma un ángulo de 58°, con el suelo, encuentre la longitud del cable.
El cable mide 75,48 metros
3) Desde el lugar donde me encuentro, la visual de la torre forma un ángulo de 32° con la horizontal. Si me acerco 25 m, el ángulo es de 50°. ¿Cuál es la altura de la torre?.
La altura de la torre es 32,84 m.
4) Dos edificios distan entre sí 150 metros. Desde un punto del suelo que está entre los dos edificios, vemos que las visuales a los puntos más altos de estos forman con la horizontal ángulos de 35° y 20°. ¿Cuál es la altura de los edificios, si sabemos que los dos miden lo mismo?
La altura de los dos edificios es de 35,92 m.

