¿Qué es una fracción?

1- Definición

Una fracción es un número, que se obtiene de dividir un entero en partes iguales. Por ejemplo cuando decimos una cuarta parte de la torta, estamos dividiendo  la torta en cuatro partes y consideramos una de ellas.
 

Una fracción se representa matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada raya fraccionaria.

La fracción está formada por dos términos: el numerador y el denominador. El numerador es el número que está sobre la raya fraccionaria y el denominador es el que está bajo la raya fraccionaria.

El numerador es el número de partes que se considera de la unidad o total.

El denominador es el número de partes iguales en que se ha dividido la unidad o total.

 

 

 

2- Lectura de fracciones

Todas las fracciones reciben un nombre específico, se pueden leer como tal, de acuerdo al numerador y denominador que tengan.

El número que está en el numerador se lee igual, no así el denominador. Cuando el denominador va de 2 a 9, tiene un nombre específico:
 

Denominador	Se lee	Ejemplo
2	medios	$\frac{1}{2} \to$ un medio
3	tercios	$\frac{2}{3} \to$dos tercios
4	cuartos	$\frac{4}{4} \to$ cuatro cuartos
5	quintos	$\frac{3}{5} \to$ tres quintos
6	sextos	$\frac{5}{6} \to$ cinco sextos
7	séptimos	$\frac{6}{7} \to$  seis séptimos
8	octavos	$\frac{5}{8} \to$  cinco octavos
9	novenos	$\frac{4}{9} \to$ cuatro novenos

Sin embargo, cuando la cifra del denominador es mayor que 10 se le agrega al número la terminación "avos".

Ejemplos:
 

$\frac{5}{12}$ = cinco doceavos

$\frac{3}{20}$ = tres veinteavos
 

En el caso particular de las fracciones con denominador 10 ,100 y 1 000 se lee “décimos”, “centésimos” y “milésimos” respectivamente.

Ejemplos:
 

Denominador	Se lee	Ejemplo
10	décimos	$\frac{4}{10} \to$ cuatro décimos
100	centésimos	$\frac{2}{100} \to$ dos centésimos
1 000	milésimos	$\frac{3}{1 000}\to$  tres milésimos

 

3- Representación de fracciones

Las fracciones se pueden representar de las siguientes maneras:

3.1- Modelo de área
Se representan los enteros con figuras geométricas que se dividen en partes iguales. Las figuras pueden ser cuadrados, rectángulos, círculos, entre otros.

Ejemplo: $\frac{3}{4}$

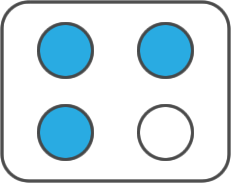
3.2- Conjunto
Consiste en una colección de elementos individuales. El denominador de la fracción indica la cantidad total de elementos y el numerador  representa la cantidad de elementos que se consideran del conjunto.

Ejemplo: $\frac{3}{4}$

 

3.3- Recta numérica
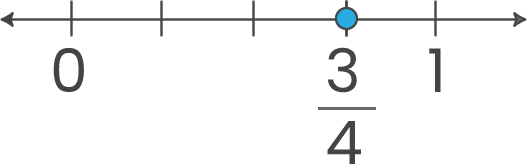
Corresponde a identificar cada fracción con un punto de la recta numérica.
Para representar fracciones en la recta numérica se divide la unidad (entero) en segmentos iguales, como indica el denominador, y se ubica la facción según indica el numerador.

Ejemplo: $\frac{3}{4}$

 

 

4- Los significados de las fracciones en los distintos contextos de uso

4.1 La fracción como expresión que vincula la parte con el todo
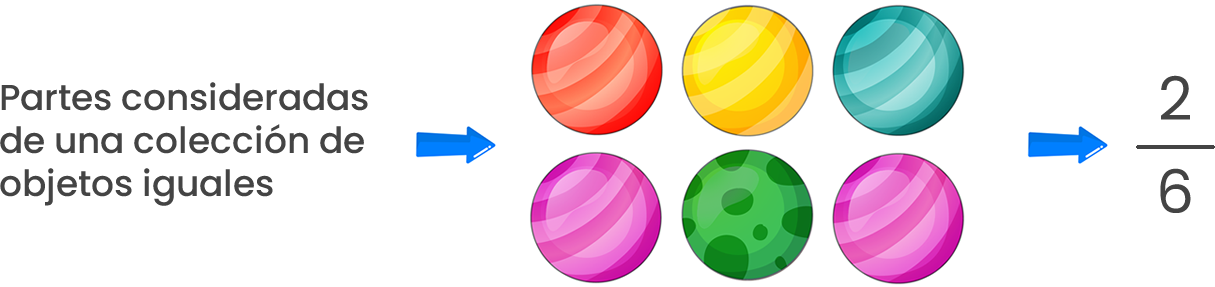
En este caso se la utiliza para indicar “la fractura” o “división en partes”, respondiendo a la pregunta ¿qué parte es? del entero en cuestión o como partes consideradas de una colección de objetos  iguales. Se conviene que el denominador de la fracción indica el número de partes en que está dividido dicho entero y el numerador las partes consideradas.

Por ejemplo:

– ¿ Qué parte de este grupo de pelotas es color rosa? 
 

 

 

 4.2- La fracción como cociente o reparto equitativo
En este caso, la fracción $\frac{a}{b}$ representa el resultado de repartir equitativamente una cantidad “a” en “b” partes iguales. Responde a la pregunta: ¿cuánto le corresponde a cada uno?

Por ejemplo, al repartir 3 barras de chocolate entre 2 niños, cada uno recibirá $\frac{3}{2}$ de barra.

1.° Se reparte 1 barra de chocolate a cada uno.

2.° La barra de chocolate sobrante se reparte por la mitad.
 

Veamos otra situación:

Un grupo de 4 amigos se reúnen a comer. Tienen 3 pizzas, las que repartirán  en partes iguales. ¿Qué fracción de pizza le corresponde a cada uno?

 

 

Como la división 3 : 4 no es exacta, debemos hacer lo siguiente:

 1.° Dividiremos cada pizza en 4 partes iguales, es decir, en cuartos.

 

 

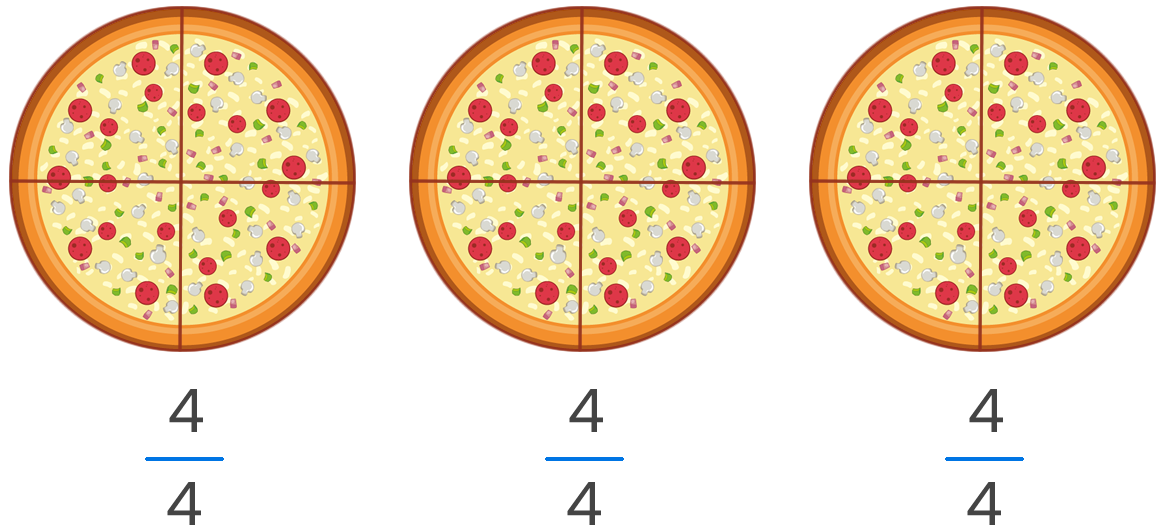
2.° Luego se reparten los 12 pedazos entre los 4 amigos.
 

 

 

 

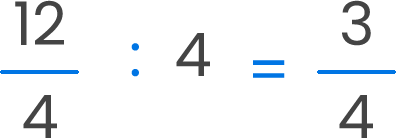
4.3-  La fracción como razón
Una razón es una comparación entre dos cantidades mediante un cociente. 

Se pueden comparar:

– Dos conjuntos distintos, por ejemplo, la razón o relación entre número de libros en la clase y número de alumnos. Así, 13 libros para 26 alumnos podrá expresarse como $\frac{13}{26}$ leyéndose “13 a 26” ó lo que es lo mismo, “1 por cada 2”.
 

– Un conjunto y un subconjunto del mismo, por ejemplo, la relación entre los 21 alumnos en total y los alumnos varones (11) de una clase puede expresarse como $\frac{11}{21}$ o “11 a 21”. Un caso especial lo constituye la probabilidad definida como el número de casos favorables sobre el número de casos posibles de un evento determinado. Por ejemplo, en la tirada de un dado la probabilidad o razón de probabilidad de que salga un 2 “es uno a 6” lo cual se indica como $\frac{1}{6}$.

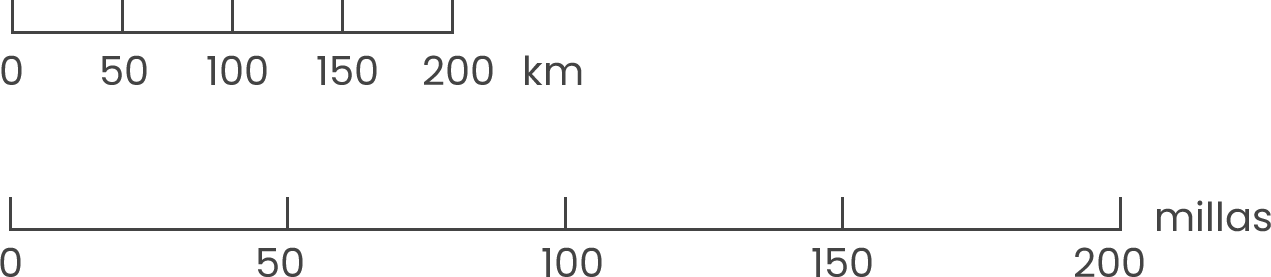
– Dos medidas según una unidad de medida común, por ejemplo, podremos afirmar que Juan tiene una altura equivalente a $\frac{2}{3}$ de la de Pedro (en cm) o que la escala (razón entre la distancia entre dos puntos determinados en el mapa y su distancia real) es 1 sobre 1 000 000, lo que puede significar que un milímetro en el mapa corresponde a un kilómetro en la realidad. Ejemplos de presentación de escalas: 1 cm representa 100 km y una pulgada representa 100 millas:
 

 

4.4- La fracción como operador
En este caso la fracción actúa sobre otro número para transformarlo. Por ejemplo, cuando te piden calcular los $\frac{4}{5}$ de 20 o los $\frac{3}{4}$ de 56.
 

Ejemplo:

$\frac{3}{4}$ de los estudiantes de un curso son varones. Si en total hay 36 estudiantes, ¿cuántos varones son?

En este caso, el número 36 debe ser multiplicado por 3 y dividido por 4, o equivalentemente dividido por 4 y el resultado, multiplicado por 3.

 

 

3.5- Fracción como medida
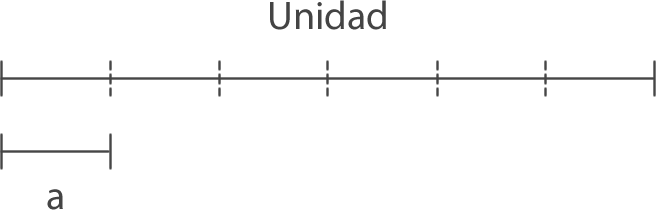
Este tipo de fracciones se emplea cuando se quiere medir una determinada magnitud, pero la unidad no está contenida un número entero de veces en la magnitud que se desea medir.

Ejemplo:
La longitud del segmento “a” corresponde a $\frac{1}{6}$ de unidad, porque si repetimos 6 veces esa medida obtenemos la unidad.

 

 

 

 

– Fracciones: términos lectura y escritura.