1- Espacio muestral
Para poder realizar el cálculo de una probabilidad es necesario determinar el espacio muestral del experimento y la cardinalidad de este mismo. (#).
El espacio muestral son todos los casos que surgen al realizar el experimento definido.
Ejemplo 1:
Se realiza el experimento de lanzar un dado al aire. Determine el espacio muestral y la cardinalidad de este.
Solución:
Como sabemos al lanzar el dado se pueden obtener números del 1 al 6. Por lo tanto:
E=1; 2; 3; 4; 5; 6 ;# =6
Ejemplo 2:
Se realiza el experimento de extraer una bolita de una bolsa que tiene bolas negras y blancas. Determine el espacio muestral del experimento.
Solución:
En la bolsa tenemos bolas negras y blancas por lo tanto el espacio muestral quedaría:
E=negras; blancas
2- Diagrama de árbol
El diagrama de árbol es una técnica para poder definir el espacio muestral del experimento cuando se realizan más de un experimento de manera consecutiva.
Este diagrama sirve para poder definir todas las posibles combinaciones que se pueden obtener al entrelazar los experimentos determinados.
La particularidad del diagrama de árbol es mostrar de manera visual todas las combinaciones que se van generando.
Ejemplo 3:
Se realiza el experimento de lanzar un dado y luego una moneda. Determine el espacio muestral del experimento. Aplicando la técnica de diagrama de árbol.
Solución:
En este caso tenemos dos experimentos que se realizan de manera consecutiva.
Primero el lanzamiento del dado y luego el lanzamiento de la moneda. Para poder determinar el diagrama de árbol. Debemos primero determinar el espacio muestral de cada experimento de manera independiente y luego entrelazamos ambos experimentos.
Elanzar un dado= {1,2,3,4,5,6} → #lanzar un dado = 6
Elanzar una moneda = {cara; cruz}→ #lanzar una moneda = 2
Ahora vamos a entrelazar los experimentos:
– La primera posibilidad es que salga el numero 1 al lanzar el dado y cara al lanzar la moneda.
– La segunda posibilidad es que salga el numero 1 al lanzar el dado y cruz al lanzar la moneda.
– La tercera posibilidad es que salga el numero 2 al lanzar el dado y cara al lanzar la moneda.
– La cuarta posibilidad es que salga el numero 2 al lanzar el dado y cruz al lanzar la moneda.
Así sucesivamente quedando el diagrama de árbol de la siguiente manera.
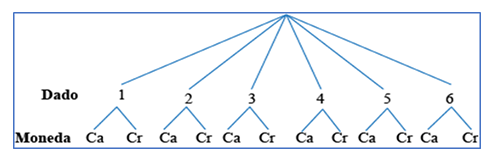
Ahora podemos determinar el espacio muestral el cual sería:
Elanzar dado y moneda = {1, cara – 1, cruz – 2, cara – 2, cruz – 3, cara – 3, cruz – 4, cara – 4, cruz – 5, cara – 5, cruz – 6, cara – 6, cruz}
Ejemplo 4:
Se realiza un experimento de extraer dos bolitas de una bolsa que contienen bolas rojas, verdes y negras. Determine el espacio muestral y su diagrama de árbol del experimento.
Solución:
En la bolsa tenemos 3 tipos de bolitas por lo tanto en la primera extracción se puede obtener cualquiera de esas tres bolitas, pero en la segunda extracción como es la misma bolsa entonces también nos puede salir cualquiera de esas tres opciones de bolitas. Por lo tanto, solo debemos entrelazar las posibilidades quedando el siguiente diagrama de árbol:
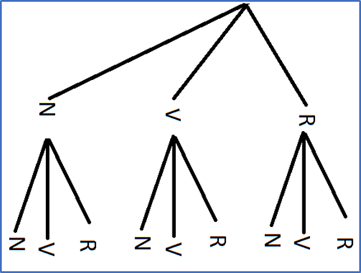
El espacio muestral quedaría:
Eextraer bolitas de una bolsa = { RR-RV-RN-VR-VV-VN-NR-NV-NN }
3- Principio multiplicativo
El problema del diagrama de árbol existe cuando se realizan más de 2 experimentos sucesivamente ya que queda muy extenso el diagrama y poco entendible.
Por ende, se determina una técnica denominada “principio multiplicativo”.
El principio multiplicativo: “Es una técnica de conteo que sirve para poder determinar la cardinalidad de experimentos que suceden de manera consecutiva. También es conocido como el principio fundamental de la combinatoria”.
Si tenemos un experimento que consta de tres sucesos el primero tiene
N1
elementos, un segundo evento que tiene
N2
elementos y un tercer evento de N_3 elementos. Entonces la cardinalidad del experimento se determina como:
#Experimento=N1·N2·N3
A modo general si tenemos un experimento con k sucesos, su cardinalidad se determina como:
#Experimento=S1·S2·S3·S4·…………·SK
Ejemplo 5:
Una persona desea construir una casa, para lo cual considera que puede construir los cimientos de su casa de cualquiera de las dos maneras (concreto o block de cemento), mientras que las paredes las puede hacer de adobe, adobón o ladrillo, el techo puede ser de concreto o lámina galvanizada y por último los acabados pueden realizarse de una sola manera
¿Cuántas formas tiene esta persona para poder construir su casa?
Solución:
Debemos considerar que para poder construir su casa debe pasar por 4 etapas:
a- Cimiento (C)
b- Paredes (P)
c- Techo (T)
d- Acabado (A)
Para cada uno de estas etapas tiene sus respectivas posibilidades.
a- Cimiento:
– Concreto.
– Block.
b- Paredes:
– Adobe.
– Adobón.
– Ladrillo.
c- Techo:
– Concreto
– Lámina galvanizada
d- Acabados
Entonces cada etapa nos queda de la siguiente manera:
C = 2
P = 3
T = 2
A = 1
Aplicando el principio multiplicativo nos quedaría:
Cardinalidad=C·P·T·A Cardinalidad= 2·3·2·1 Cardinalidad=12
Es decir, esta persona tiene 12 formas distintas de construir su casa.
Ejemplo 6:
¿Cuántos números de teléfonos de seis dígitos se pueden formar con los números del 0 al 9? ¿Considerando que el 0 no puede estar al inicio y no es posible repetir los dígitos?
Solución:
Primero debemos tomar en cuenta que del 0 al 9 existen 10 dígitos. En el problema tenemos dos condiciones.
– La primera dice que el 0 no puede estar como primer digito, por lo tanto, para el primer digito solo tenemos 9 posibilidades.
Primer digito = 9 posibilidades.
– Para el segundo digito tenemos el número 0 y 8 dígitos (ya que uno se utilizó en el primer digito).
Por lo tanto, para el segundo digito tenemos 9 posibilidades (8 restantes+ el digito 0 que no se podía ocupar).
Segundo digito = 9 posibilidades.
Ya tenemos ocupados dos dígitos de los 10 que teníamos al inicio, por lo tanto, para el tercer digito tenemos solo 8 posibilidades.
Tercer digito = 8 posibilidades.
Y así sucesivamente vamos descontando un digito que ya está utilizado. Por ende:
Cuarto digito =7 posibilidades.
Quinto digito =6 posibilidades.
Sexto digito =5 posibilidades.
Aplicando el principio multiplicativo nos queda:
#Cantidad de números telefónicos =9·9·8·7·6·5#Cantidad de números telefónicos = 136 080 números telefónicos.

