1- Polígonos
En primer lugar veremos lo relacionado con los polígonos.
El perímetro de un polígono corresponde a la medida del contorno de una figura geométrica y se calcula sumando la medida de todos sus lados. El área es la medida de la región o superficie encerrada por un polígono.
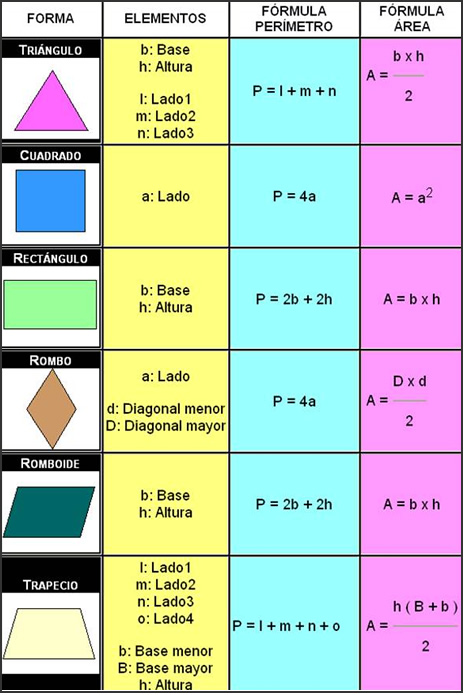
2- Área y perímetro de paralelogramos
– Cálculo del perímetro
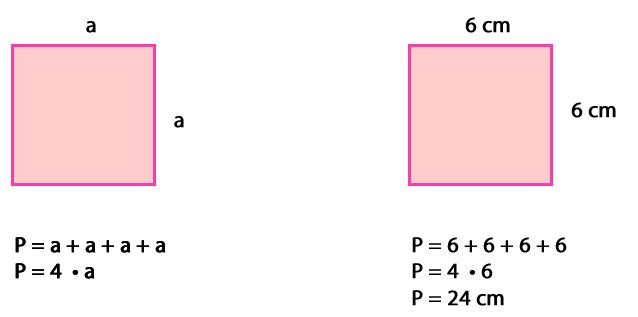
Entonces, para calcular el perímetro de un cuadrado se puede emplear la fórmula:
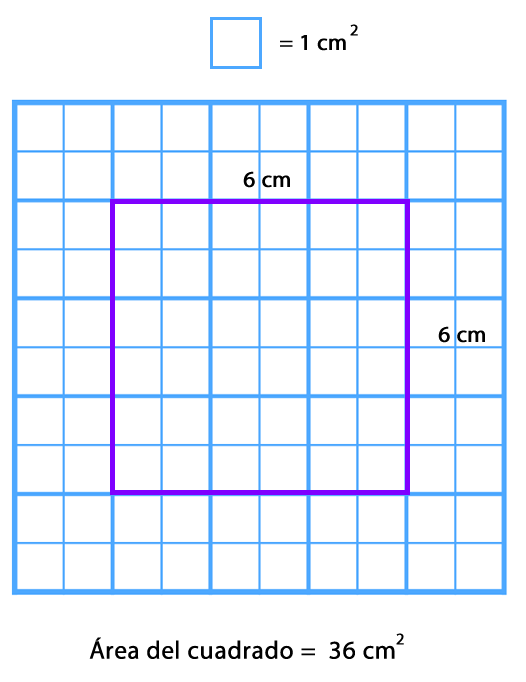
Como puedes observar, para calcular el área de un cuadrado se multiplica la medida de su base por la de la altura, es decir, su largo por su ancho.
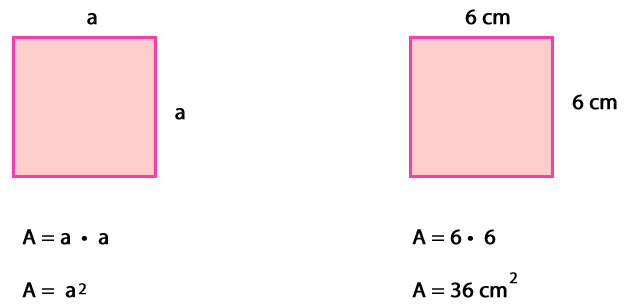
Entonces, para calcular el área del cuadrado se puede aplicar la fórmula:
2.2- Rectángulo
– Cálculo del perímetro
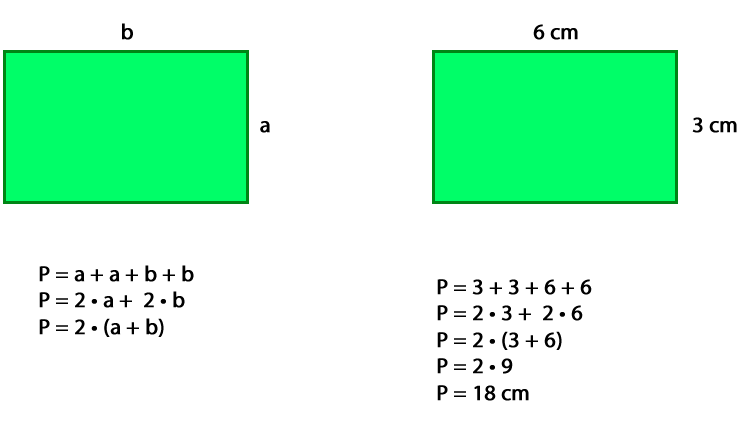
El perímetro del romboide es igual a la suma de las longitudes de sus cuatro lados.

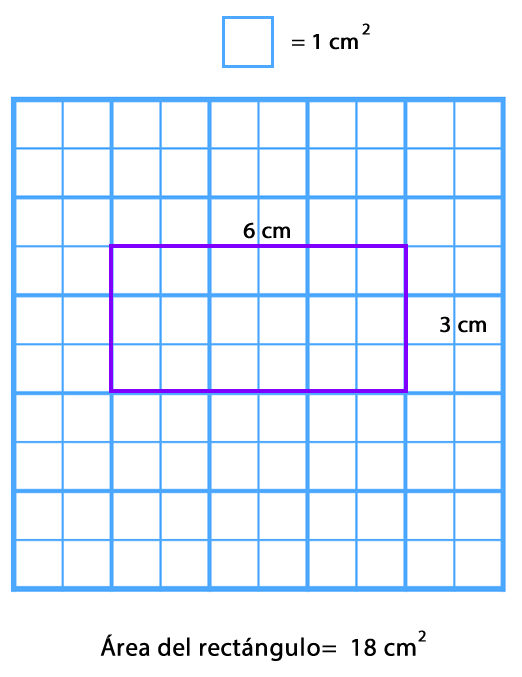
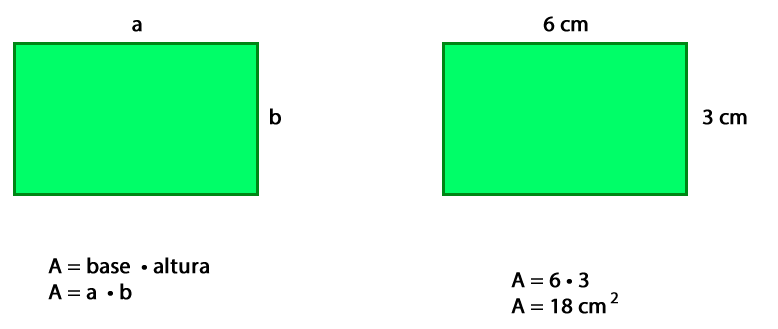
– Cálculo del área
Representación cuadrícula
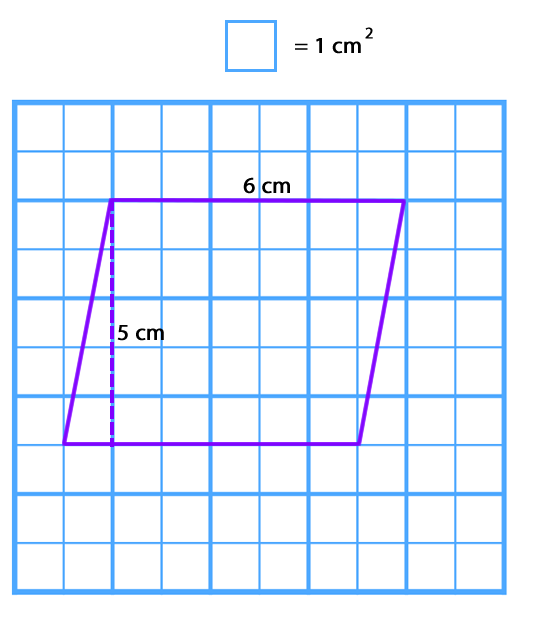
Para calcular el área del romboide en una cuadrícula se puede descomponer la figura formando dos triángulos rectángulos y un cuadrado o rectángulo.
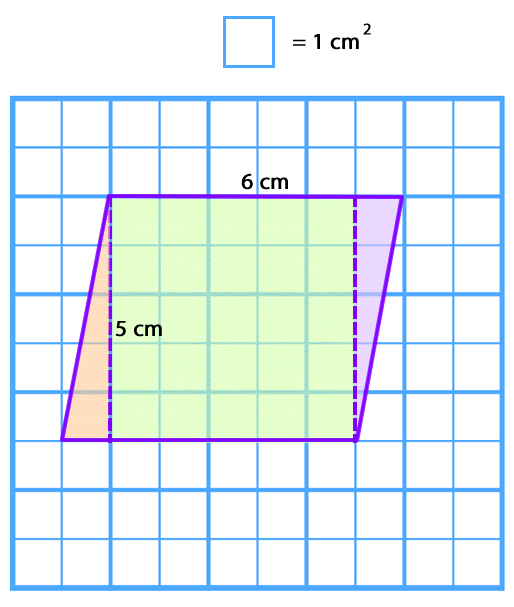
Luego, se traslada uno de los triángulos rectángulos para formar un rectángulo.
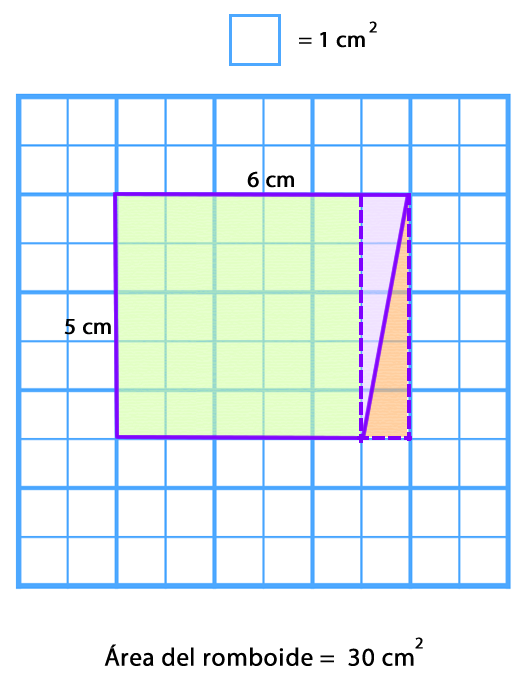
Se contabiliza la cantidad de cuadrados que contiene el romboide y su área corresponde a 30 cm2.
El área del romboide se obtiene a partir del área del rectángulo, multiplicando la base por la altura del romboide (no por el otro lado).
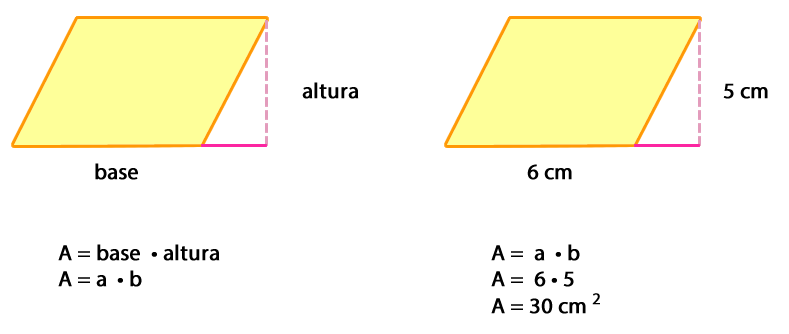
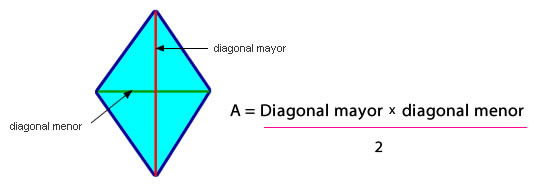
2.4- Rombo
– Cálculo del perímetro
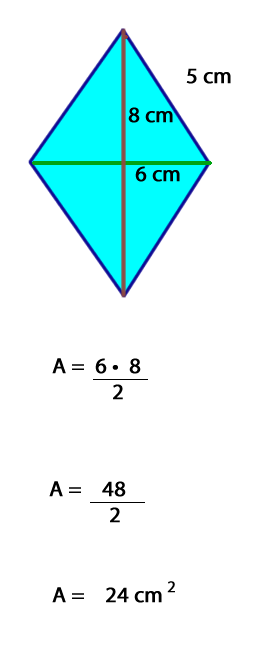
Sumando las longitudes de los lados de un polígono hallaremos su perímetro. Otra forma de calcularlo es multiplicando la medida de su lado por 4.
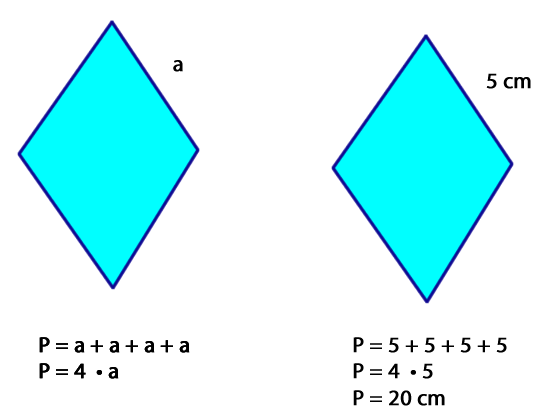
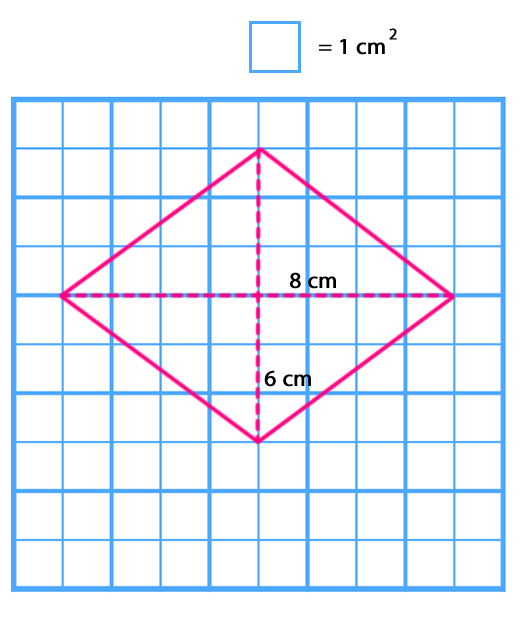
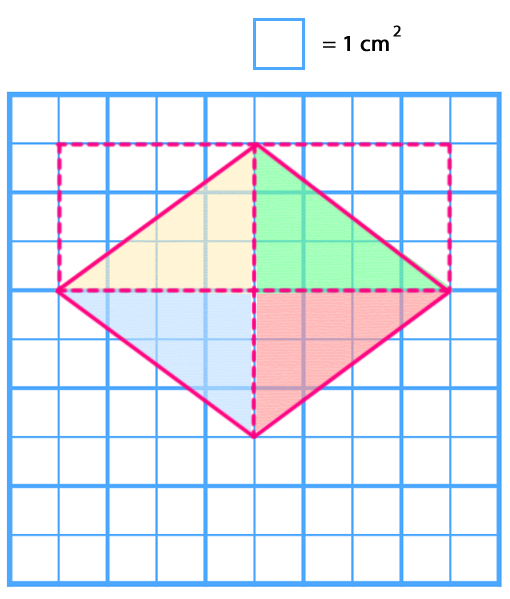
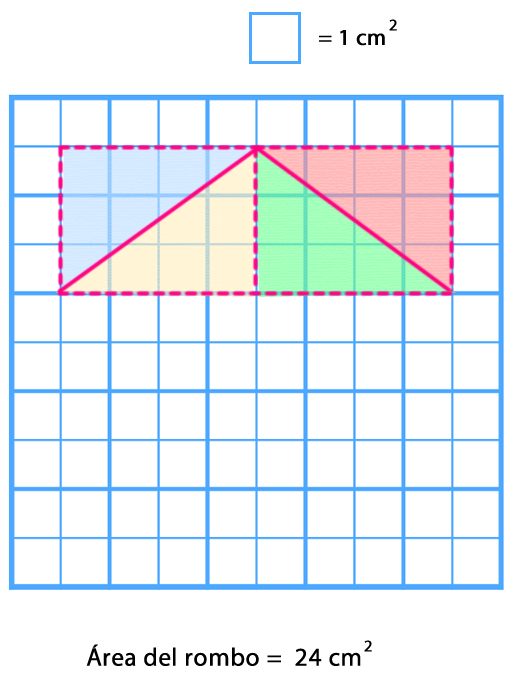
Para calcular el área del rombo en una cuadrícula se puede descomponer la figura formando cuatro triángulos rectángulos.
3- Área y perímetro del triángulo
– Cálculo del perímetro

– Cálculo del área
Representación cuadrícula
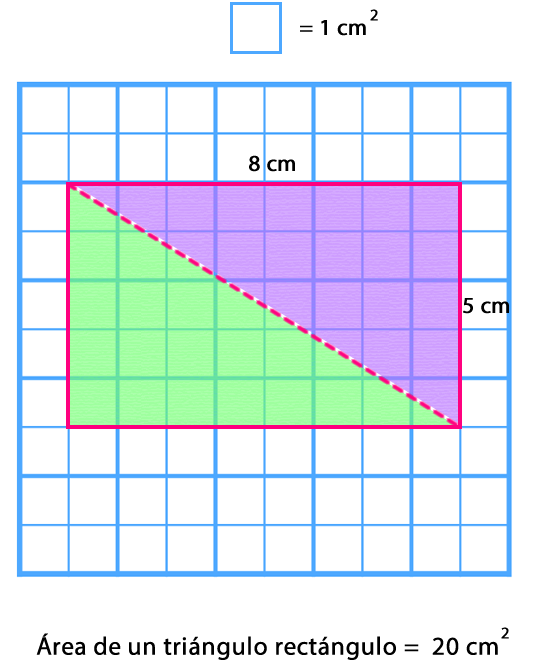
Si se representa un rectángulo y se traza una diagonal se puede observar que se forman dos triángulos rectángulos congruentes.
Entonces, se puede afirmar que para calcular el área de un triángulo, primero se determina el área del rectángulo y la mitad de esta medida corresponderá al área de un triángulo rectángulo.
Si se tiene un triángulo cualquiera también se puede aplicar esta lógica.
El triángulo presentado se descompone en más triángulos.
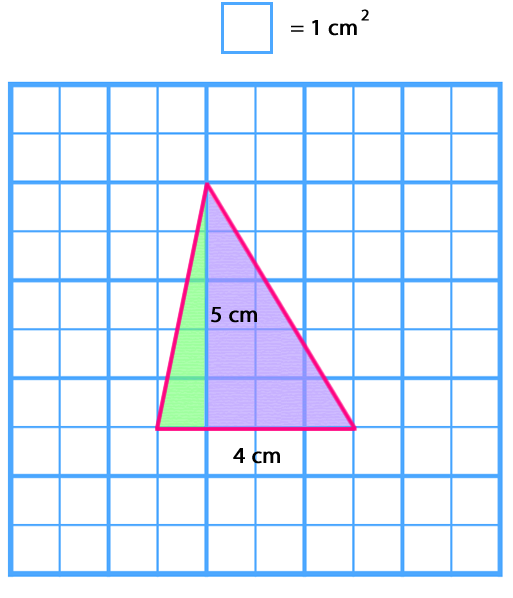
Luego, los triángulos se reflejan formando un rectángulo.
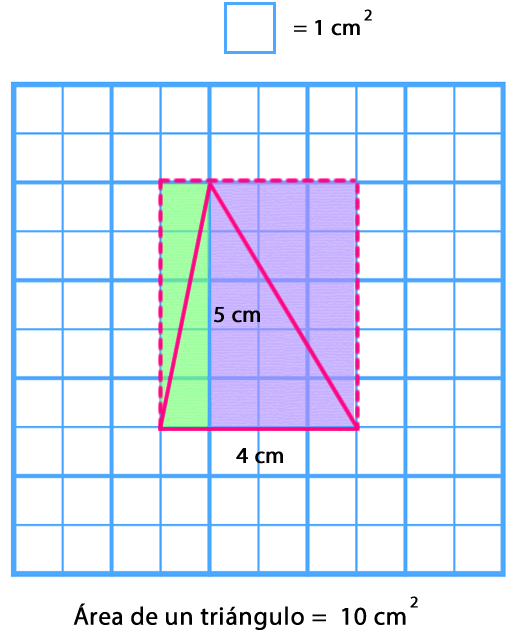
Por lo tanto, para calcular el área se multiplica uno de sus lados por la altura y su resultado se divide por dos.
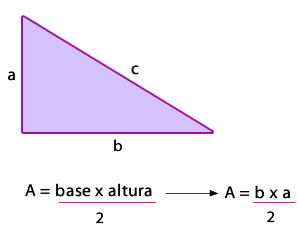
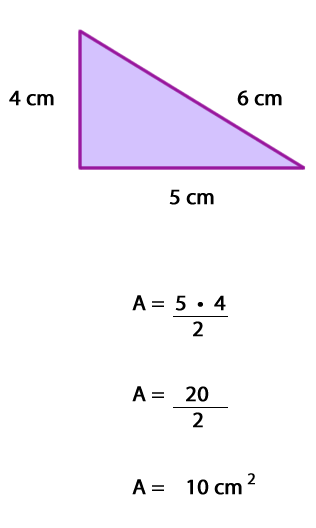
Ejemplo:
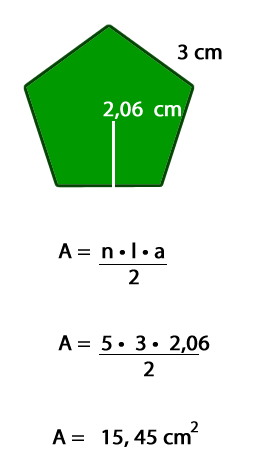
5- Resolución de problemas
a- En el terreno que se aprecia en la imagen se instalará un cerco con una malla. ¿Cuántos metros de malla son necesarios para instalar el cerco?
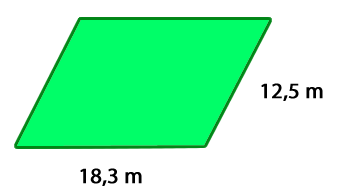
La situación está relacionada con el cálculo de perímetro, para conocer la cantidad de metros de malla necesarios para instalar el cerco, se suma la longitud de todos los lados.
Respuesta: Se necesitan 61, 6 m de malla para cercar el terreno.
b- Mario quiere embaldosar un piso rectangular que tiene 5 m de largo y 3 m de ancho. Las baldosas son cuadradas de lado 20 cm. ¿Cuántas baldosas son necesarias para cubrir la superficie del piso?
La situación se asocia al cálculo del área. Se debe calcular el área del piso rectangular y de las baldosas.
Nota: Para resolver la situación debes convertir las unidades correspondientes, ya sea a metros o centímetros.
En este caso se convertirá de m a cm, multiplicando los números por 100.
Largo: 5m = 5 100 = 500
Ancho: 3m = 3 100 = 300
Área del piso:
Área de cada baldosa:
Para conocer la cantidad de baldosas que se utilizarán se dividen ambas áreas:
Respuesta: Se necesitan 375 baldosas para cubrir la superficie del piso.
c- Una cancha rectangular de 20 m de largo y 12 m de ancho se cubre con trozos de pasto sintético. Si cada trozo de pasto sintético mide 2 m de largo y 2 m de ancho, y el valor de cada uno es de $5 230. ¿Cuánto hay que pagar para cubrir la cancha?
La situación se relaciona con el cálculo de área.
Área de la cancha:
Área de un trozo de pasto sintético:
Para conocer la cantidad de trozos de pasto sintético que se utilizarán para cubrir la cancha, se dividen ambas áreas:
Finalmente, se multiplica $5 230 por 60 para conocer el precio total.
Respuesta: Para cubrir la cancha se necesitan $313 800.
d- Carolina y Claudio están confeccionando banderines de género con forma de triángulo para un evento deportivo. Si ellos tienen que hacer 100 banderines iguales a los de la imagen. ¿Cuántos metros cuadrados de género ocuparán?
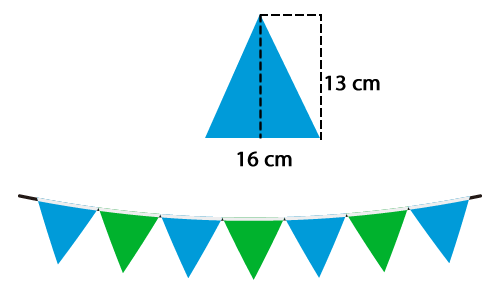
Antes que todo se debe identificar qué tipo de cálculo se debe efectuar. En esa situación están solicitando los metros cuadrados de género que se ocuparán para confeccionar banderines.
Por lo tanto, se calcular el área de un triángulo.
A continuación, se multiplica la cantidad de banderines por el área de un triángulo.
Finalmente, se convierten los cm2 a m2 dividiendo el número por 10 000.
Respuesta: Se necesitarán 1,04 m2 de género para confeccionar los banderines.

