1- Suma y resta de números enteros
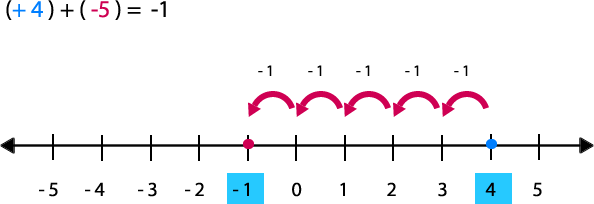
Se ubica + 4 en la recta numérica y como 5 es negativo, se deben contar 5 unidades hacia la izquierda. La posición final corresponde a -1.
Ejemplo 2: (-4) + (-5)
La posición final es -9.

1.2- ¿Cómo resolver adiciones de números enteros de manera simbólica?
Para sumar dos números enteros:
1.3- Representación de sustracción de números enteros en la recta numérica
Para representar la sustracción en la recta numérica, primero que todo debes ubicar los números del minuendo y el sustraendo. Posteriormente, se cuentan las unidades que hay entre una cantidad y otra, siempre comenzando desde la posición del sustraendo.
Hay que considerar que el conteo hacia la derecha indica una cantidad positiva, mientras que el conteo hacia la izquierda indica una cantidad negativa.
Ejemplo: 2 -(-3)
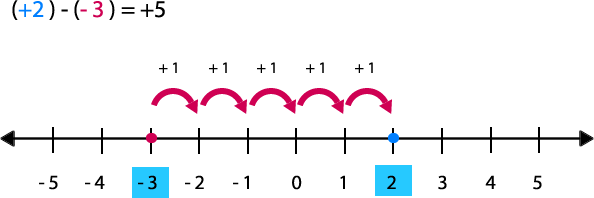
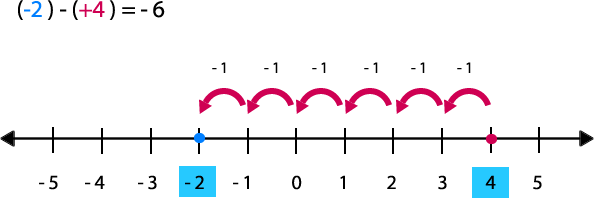
Desde 4 (sustraendo) hasta -2, hay 6 unidades de diferencia y como el conteo es hacia la izquierda, el número tendrá signo negativo.
1.4- ¿Cómo resolver sustracciones de números enteros de manera simbólica?

3.1- Representación de multiplicaciones de números enteros en la recta numérica
Para representar multiplicaciones de números enteros positivos se puede realizar de la siguiente manera:
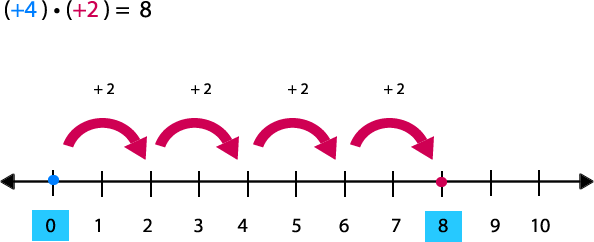
Ejemplo: (+4)
· (+2)
La multiplicación es una suma iterada, en este caso se suma 4 veces el número 2 comenzando desde 0. Si observas, el conteo va de 2 en 2
La posición final es +8.
Cuando se multiplica un número natural positivo por un número negativo, también se puede representar como suma iterada.
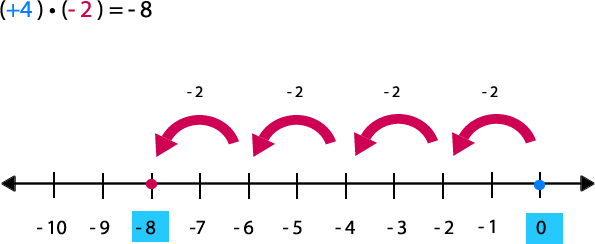
Ejemplo: 4
·(-2)
En este caso, la suma iterada es:
4 • (-2) = (-2) + (-2) + (-2) +(-2) = – 8
Primero, ubica el número 0 y suma 4 veces -2. Recuerda realizar el conteo comenzando desde 0 hacia la izquierda.
La posición final corresponde a -8.
1.4- ¿Cómo resolver de manera simbólica la multiplicación de números enteros?
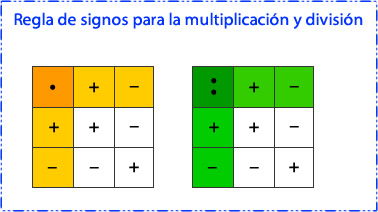
Regla de los signos:
Ejemplo: 9 : 3
1- Trazar un segmento desde 0 hasta 9, que es la cantidad indicada en el dividendo.
2- Dividir la recta numérica según la cantidad que indique el divisor, es decir, en 3 segmentos de la misma medida.
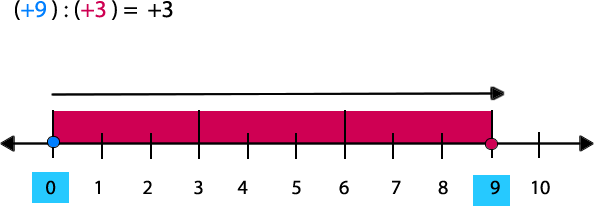
3- Observar el número que se encuentra ubicado en la primera división como se indica en la imagen. En este caso es 3.

Para representar en la recta numérica la división de un número entero negativo por un número natural, se realiza un procedimiento similar al anterior:
Ejemplo: (-9) : 3
1- Trazar un segmento desde 0 hasta -9.
2- Dividir la recta numérica según la cantidad que indique el divisor, en este caso, 3 segmentos con la misma longitud.
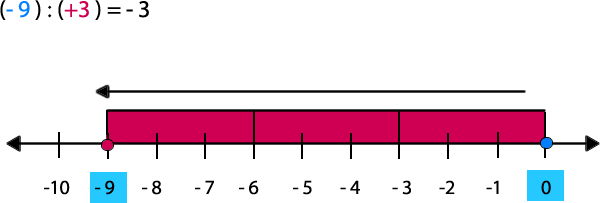
3- Observar la ubicación del número en donde se encuentra la primera división. Dicho número corresponde al cociente de la división.

3.3- ¿Cómo resolver la división de números enteros de manera simbólica?
a) (–3 + 5)
·
(–3) : 2 + (–1 + 6) Respuesta: 2
b) 12 : 2 : (–6 + 8) Respuesta: 3
5- Apliquemos lo aprendido
a) Si a= 13, b = – 25 y c = -72. ¿Cuál es el valor de a + b – c + b?
Para resolver el ejercicio se reemplazan los valores en la expresión y se obtiene lo siguiente:
a + b – c + b13 +(-25) – (-72) + (-25) -12
*Recuerda que debes hacer el cambio de signo cuando realizas una resta.
13 + (-25) – (-72) + (-25) -12 + 72 + -25 60 + -25 = 35
b) El producto de dos números enteros es -96. Si un factor es 4, ¿cuál es el otro factor?
Para resolver este ejercicio, se puede plantear de la siguiente manera:
x · 4 = -96
Ahora, aplicamos la operación contraria de la multiplicación para resolver el ejercicio, es decir, dividimos -96: 4.
-96 : 4 = -24
Podemos verificar si es correcto multiplicando
-24 · 4 = 96
Respuesta: El otro factor es -24.
c) Si al producto de 4 por –4 se le resta el producto de 6 por –6, entonces el resultado obtenido es igual a:
Al traducir a lenguaje matemático el enunciado, tenemos:
4 · -4 – (6 · -6)
Lo resolvemos:
4 · -4 – (6 · -6) -16 – (-36) -16 + 36 20
d) Si 6 se multiplica por –5 y se divide entre –1. ¿Cuál es el inverso aditivo del resultado?
Resolvemos el ejercicio planteado:
6 · -5 : -1 -30 : -1 = 30
Ahora, determinamos el inverso aditivo de 30. Recordemos que el inverso aditivo es el número opuesto, en este caso es -30.
Respuesta: El inverso aditivo es -30.
e) Al resolver
-24 : 2 – (-2· -4) ·-3
se obtiene:
Para resolver este tipo de ejercicios debes tener en cuenta la prioridad de las operaciones y realizar los ejercicios que están en los paréntesis más internos.
Paso 1:
-24 : 2 – (-2· -4) ·-3 8
Paso 2:
-24 : 2 – (-2· -4) ·-3 -12 – 8
Paso 3:
-24 : 2 – (-2· -4) ·-3 -12 – 8 -20
Paso 4:
-24 : 2 – (-2· -4) ·-3 -12 – 8 -20 ·-3 = 60
f) Si n, m son números enteros, n es el antecesor de m y -8 es el sucesor de m, ¿cuál es el sucesor de (n • m)?
Para resolver el ejercicio recordemos que el antecesor de un número es el que se encuentra inmediatamente a la izquierda de él en la recta numérica. Mientras que el sucesor es el que está inmediatamente a la derecha.
Según los datos que nos entregan, -8 es el sucesor de m, entonces m es -9. También se menciona que n es el antecesor de m= el antecesor de -9 es -10.

A continuación, reemplazamos los valores en la expresión:
(n · m)(-10 · -9) = 90
Por último, determinamos el sucesor de 90. El número entero que está inmediatamente a la derecha de 90 en la recta numérica es 91.
Respuesta: El sucesor es 91.

