1- Adición y sustracción de números enteros
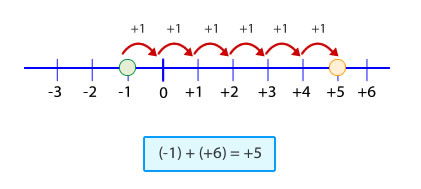
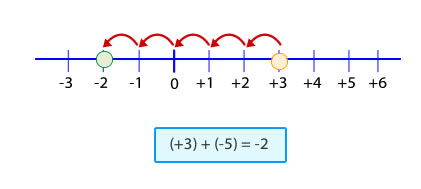
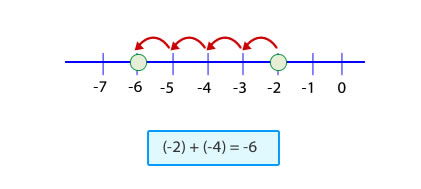
Para representar la sustracción en la recta numérica, primero que todo debes ubicar los números del minuendo y el sustraendo. Posteriormente, se cuentan las unidades que hay entre una cantidad y otra, siempre comenzando desde la posición del sustraendo.
Hay que considerar que el conteo hacia la derecha indica una cantidad positiva, mientras que el conteo hacia la izquierda indica una cantidad negativa.
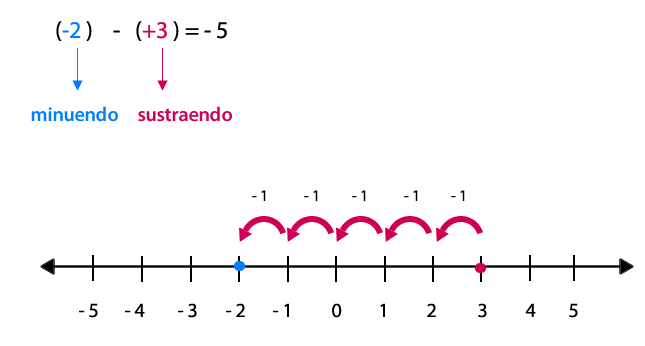
La resta se puede expresar como la suma del minuendo con el inverso aditivo del sustraendo.
En este caso:

El inverso aditivo es el número opuesto de (+ 3), en este caso correspondería a (-3).
Al resolver resulta:
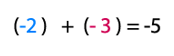
Ejemplo 2:
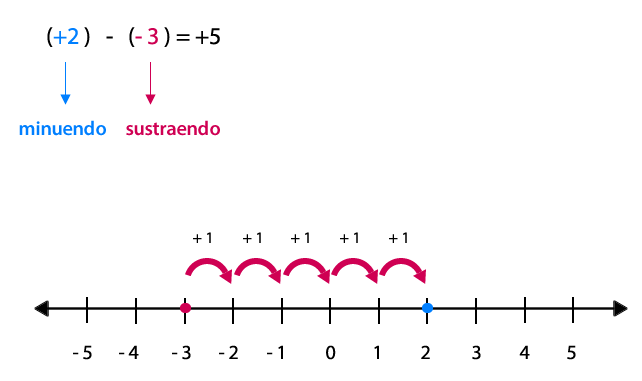
Desde -3 (sustraendo) hasta 2, hay 5 unidades de diferencia y como el conteo es hacia la derecha, el número tendrá signo positivo.
Nota: observa que restar un entero negativo es como sumar un entero positivo, y que restar un entero positivo es como sumar un entero negativo.
1.3- Ejemplos de situaciones relacionadas con adiciones y sustracciones
Veamos las siguientes situaciones:
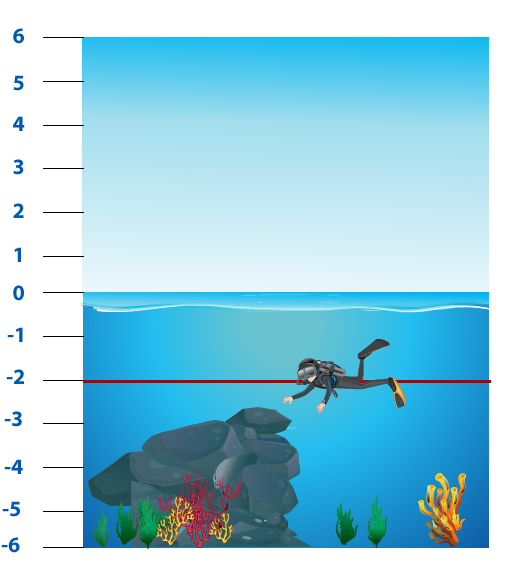
1. Un buzo se encuentra a 2 metros por debajo del nivel del mar, si el buzo desciende 3 metros más. ¿A cuántos metros de profundidad se encuentra el buzo?
Resolución:
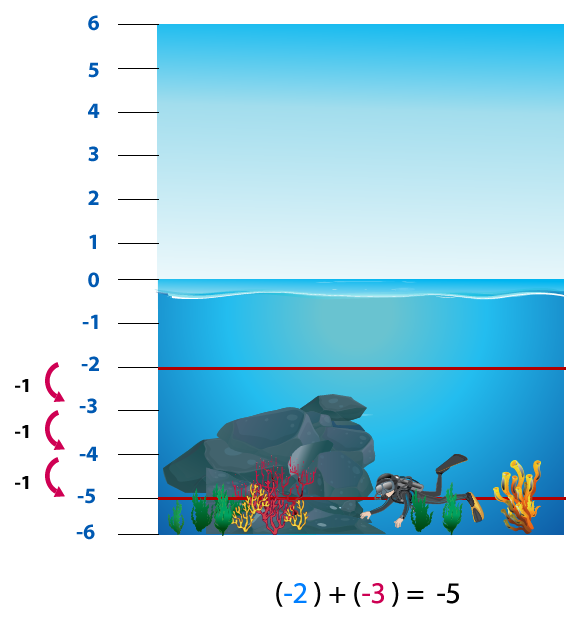
El buzo se encuentra 2 metros por debajo del nivel del mar que se puede expresar como – 2. Luego, él desciende 3 metros más, esta acción se relaciona con el signo “menos”, es decir, con -3.
Finalmente la situación puede expresarse de la siguiente manera:
(-2) + (-3) = -5
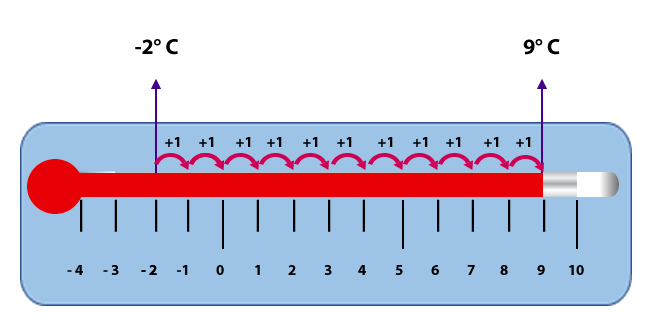
2. La temperatura mínima en una ciudad fue de -2° C, si durante el día subió 11° C. ¿Cuál es la nueva temperatura?
Resolución:
Primero ubica -2° C en el termómetro y como la temperatura subió, se cuentan 11 unidades hacia la derecha llegando a los 9°C.
3. La temperatura máxima de una ciudad fue de 4° C y la temperatura mínima fue de -3° C. ¿Cuántos grados varió la temperatura?
Resolución:
Se representan las temperaturas en los termómetros y se observa la diferencia entre estos dos.

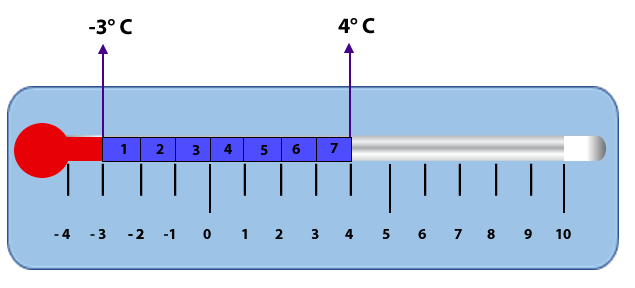
Para saber la diferencia entre un número y otro se debe realizar una sustracción.
La expresión matemática de la situación queda de la siguiente manera:
4 – (-3) = 4 + 3 = 7
2- Ejercicios combinados de números enteros
Para resolver ejercicios que tengan varias adiciones y sustracciones de números enteros, puedes utilizar las siguientes estrategias:
Estrategia 1: Sumar o restar de izquierda a derecha.
Ejemplo:
Estrategia 2: Agrupar números positivos y negativos.
Antes de aplicar esta estrategia, se cambian los signos de los números que están delante de la resta.
A continuación, sumamos los números enteros positivos.
Luego, sumamos los números enteros negativos.
Por último, realizamos la suma final. Como los números tienen diferente signo, se restan los valores absolutos y se mantiene el signo con mayor valor absoluto:
2.1- Uso de paréntesis en operaciones de números enteros
Si en un ejercicio hay paréntesis, se debe resolver primero las operaciones que están dentro de este, o bien, se pueden suprimir los paréntesis teniendo en cuenta los signos que los anteceden.
Ejemplo 1:
Como el paréntesis está antecedido por un signo “+”, estos se eliminan y los signos de los números que están en su interior, se mantienen.
Luego, se resuelve aplicando algunas de las estrategias señaladas con anterioridad:
Ejemplo 2:
Como el paréntesis está antecedido por un signo “-”, estos se eliminan y los números que están en su interior cambian por su opuesto aditivo.
Al resolver tenemos lo siguiente:
2.2– Uso de paréntesis, corchetes y llaves en operaciones de números enteros
Si en un ejercicio hay paréntesis, corchetes y llaves, resolvemos de la siguiente manera:
1.° Resolver las operaciones dentro de los paréntesis.
2.° Resolver las operaciones dentro de los corchetes.
3.° Resolver las operaciones dentro de las llaves.
4.° Resolver la adición de números enteros.

