1- Números enteros
En la vida se nos presentan muchas veces situaciones que no pueden expresarse mediante los números naturales, por ejemplo, para expresar temperaturas bajo cero, pisos subterráneos, profundidades bajo el nivel del mar, deudas, años en las líneas de tiempo, etc.
En estos casos se necesitan otro tipo de números, que son los números enteros.
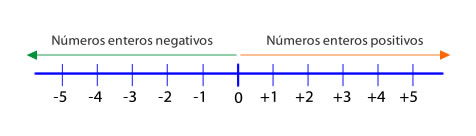
El conjunto de los números enteros (Z) es infinito y está formado por los números enteros positivos (Z+), el cero y los números enteros negativos (Z-).
→ Z+: +1, +2, +3, +4, +5, ….
→ Z-: -1, -2, -3, -4, -5, ….
→ El cero: 0 (no es positivo ni negativo)
Los números enteros negativos se escriben con un signo – delante del número.
Veamos como expresar situaciones con números enteros:
a) Alejandro Magno nació el año 356 a.C. = -356
b) La temperatura en la Antártica fue de 5 grados bajo cero: -5
c) El avión vuela a una altura de 3500 m: +3500
d) El auto está en el cuarto piso subterráneo: -4
e) Una persona ganó 2300 puntos en un juego: +2300
2- Representación gráfica y ordenación de números enteros
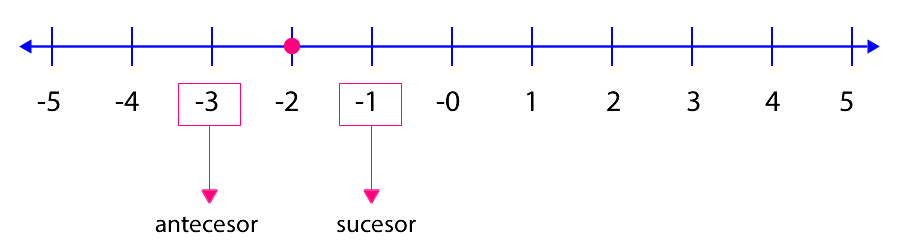
La recta numérica también nos sirve para ubicar el antecesor y sucesor de un número. El antecesor de un número es el que se encuentra inmediatamente a la izquierda de él en la recta numérica, mientras que el sucesor es el que se encuentra inmediatamente a la derecha del número en la recta numérica.
Ejemplo:
El antecesor de – 2 es –3.
El sucesor de –2 es –1.
Veamos otros ejemplos de representación de números enteros en recta numérica:
a. Ubicar -70 y 80 en la recta numérica. En este caso la recta esta graduada de 10 en 10.

b. Ubicar -140 y 60 en la recta numérica. Observa que la recta numérica está graduada de 20 en 20.

c. Ubicar -800 y 700 en la recta numérica. La recta numérica está graduada de 100 en 100.

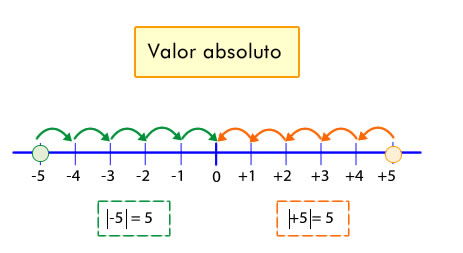
Otros ejemplos:
|-46| = 46
|0| = 0
|-179| = 179
|280| = 280
-|-654| = -654 →se conserva el signo – que antecede a |-654|
|789 – 780| = |9| = 9
Si dos números tienen igual valor absoluto y son de signos distintos, uno de ellos es el inverso aditivo del otro.
En este caso,
5 es el inverso aditivo de -5.
-5 es el inverso aditivo de 5.
Otros ejemplos:
El inverso aditivo de 45 es -45.
El inverso aditivo de -350 es 350.
El inverso aditivo de -2 342 es 2 342.
Apliquemos lo aprendido:
Si x = -6, ¿cuál es el antecesor de |x|?
Para resolver el ejercicio reemplazamos el valor de x en la expresión:
|x| = |-6| = 6
A continuación, calculamos el antecesor de 6.
El número que está inmediatamente a la izquierda de 6 en la recta numérica es 5.
4- Orden y comparación de números enteros
Representar los números enteros en la recta numérica nos sirve para poder comparar números enteros.
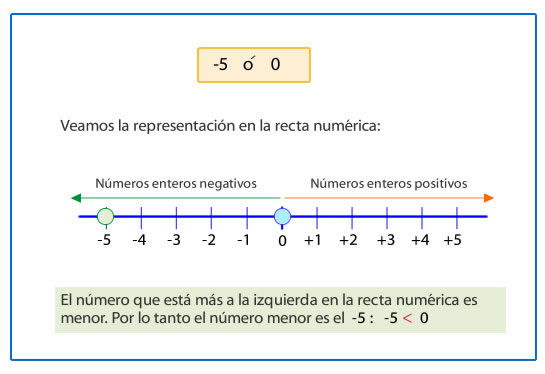

Para comparar números enteros debemos tener en cuenta lo siguiente:
– Entre dos o más números positivos, es mayor el que tiene mayor valor absoluto.
Ejemplos:
8 > 4
25 < 54
167 > 129
– Entre dos o más números negativos, es mayor el que tiene menor valor absoluto.
Ejemplos:
-2 > -5
-14 < -8
-152 > -167
– Al comparar un número positivo y uno negativo, siempre será mayor el positivo.
Ejemplos:
-8 < 2
-17 < 12
238 > -324
Teniendo en cuenta estas consideraciones podemos ordenar los números enteros. Veamos los siguientes ejemplos:
a) Ordenar de manera creciente (de menor a mayor) los siguientes números:
– 6, -10, 5, -12, 16, 13
Para resolver el ejercicio identificamos los números enteros positivos y negativos:
– 6, -10, -12 = números enteros negativos
5, 16, 13 = números enteros positivos
Comparamos los números enteros negativos:
– 12 < -10 < -6
Ahora, los positivos:
5 < 13 < 16
Finalmente, los ordenamos de manera creciente:
– 12 < -10 < -6 < 5 < 13 < 16
b) Ordenar de manera decreciente (de mayor a menor) los siguientes números.
85, -14, 140, -108, 32, – 65
Identificamos los números enteros positivos y negativos:
-14, -108, – 65 = números enteros negativos.
85, 140, 32 = números enteros positivos.
Comparamos los números enteros positivos:
140 > 85 > 32
Ahora, los negativos:
-14, > -65, > -108
Finalmente, los ordenamos de manera decreciente:
140 > 85 > 32 > -14 > -65 > -108


