Números complejos y su relación con los numeros imaginarios

1- Introducción

Un día, Florencia tuvo que resolver la siguiente ecuación: $x^2=–1$

Ella se preguntó ¿Cómo un número al cuadrado puede ser negativo?

De esta forma, cuando llegó a clases, le preguntó a su profesor por la solución de esa ecuación. A lo que él le respondió:

“¿Cuándo una ecuación no tiene solución en el conjunto numérico que estamos trabajando?”

A continuación, el profesor les fue mostrando lo siguiente:

¿Qué pasa si trabajamos en $\mathrm{\mathbb{N}}=\left\{1,2,3\dots .\infty \right\}$ (conjunto de números naturales), y debes resolver la siguiente ecuación?

$x+1=0$

Claramente esta ecuación no tiene solución en N, luego surge el conjunto de los números enteros$\mathrm{\mathbb{Z}}\left\{–\infty ,\dots .,–3,–2,–1,0,1,2,3\dots .\infty \right\}$, donde:

$x+1=0⟺x=–1$

Ahora, ¿Qué pasará en el conjunto de los números enteros con esta ecuación?

$2x=1$

Aquí, aparece el conjunto de los números racionales ($\mathrm{\mathbb{Q}}$), que da solución a la ecuación anterior, esto es $x=\frac{1}{2}$.

Luego tenemos dos tipos de ecuaciones que no tienen solución en el conjunto de los números racionales, que son las de solución del tipo:

$x=2,34562109\dots$

  
y las del tipo

$x^2=2⟺x=\pm \sqrt{2}$, sabiendo que $\sqrt{2}=1,414213562$

O sea, aquellas que tienen infinitos decimales (no periódicos ni semiperiódicos).

Aquí nace el conjunto de los números irracionales $\left(Q^{*}\right)$.

Todos estos conjuntos numéricos que has estudiado hasta ahora, reciben el nombre de “Conjunto de Números Reales” $\left(\mathrm{ℝ}\right)$.

1.1 “Representación de los Números Reales”

 
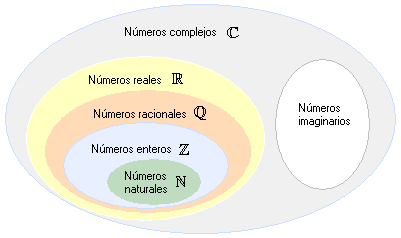
Explicado este esquema del conjunto de los números reales, Florencia preguntó: ¿Qué significa la $\mathrm{ℂ}$ que está arriba?

Ahora el profesor le mostró la ecuación que ella llevó a la clase, que es:

$x^2=–1$

que tendría como solución: 

$x=\sqrt{–1}$

Aquí nace el “Conjunto de los Números Complejos ($\mathrm{ℂ}$) que incluye la unidad imaginaria como $\sqrt{–1}$ que se representa con la letra i.
 

2. “Conjunto de los Números Complejos”

Resolvamos las siguientes ecuaciones en el conjunto de los números reales:

Recordemos que una ecuación cuadrática es de la forma:

$a{x}^2+bx+c=0\leftrightarrow x=\frac{–b\pm \sqrt{b^2–4ac}}{2a}$ donde 

Donde$∆=b^2–4ac$ , llamado discriminante y en el conjunto de los números complejos, cantidad subradical

Aquí teníamos los siguientes casos:

Si $∆ >0\Rightarrow$ la ecuación tenía dos soluciones reales y distintas.
Si $∆ =0\Rightarrow$ la ecuación tiene 1 solución real.

Si $∆ <0\Rightarrow$ la ecuación no tiene soluciones reales es aquí donde comenzamos a estudiar los números imaginarios y complejos.

Resolvamos:

1)   $x^2–2x+5=0$; donde $a=1$; $b=–2$ y $c=5$

$$\begin{gathered} x=\frac{+2\pm \sqrt{{\left(–2\right)}^2–4·1·5}}{2·1} \\ x=\frac{2\pm \sqrt{4–20}}{2} \end{gathered}$$

$x_1=\frac{2+\sqrt{–16}}{2}$   $\wedge$ $x_2=\frac{2–\sqrt{–16}}{2}$

En esta ecuación tenemos dos soluciones complejas y distintas.

¿De qué otra forma podemos escribir estas soluciones?

Recordemos que$i=\sqrt{–1}$ ; entonces $\sqrt{–16}=\sqrt{–1}\sqrt{16}$ luego aplicamos la notación utilizando la unidad imaginaria: $4i$ 

Luego las soluciones $x_1=\frac{2+4i}{2}$ ∧ $x_2=\frac{2–4i}{2}$; simplificamos y nos queda:

$x_1=1+2i$ ∧ $x_2=1–2i$

2)   $x^2+x+1=0$; donde $a=1$;$b=1$ y $c=1$

$$\begin{gathered} x=\frac{–1\pm \sqrt{1^2–4·1·1}}{2·1} \\ x=\frac{–1\pm \sqrt{1–4}}{2} \end{gathered}$$

$x=\frac{–1\pm \sqrt{–3}}{2}$ luego,   $\sqrt{–3}=\sqrt{3·–1}=\sqrt{3}i$

$\iff x_1=\frac{–1+\sqrt{3}i}{2}\wedge x_2=\frac{–1–\sqrt{3}i}{2}$

2.1 Partes de un Número Complejo

Un número complejo, como vimos en el primer ejemplo, tiene como solución 1-2i. Este número complejo tiene una parte real y una parte imaginaria, que son:

• Parte real: 1
• Parte imaginaria -2

Podemos entonces generalizar que un número complejo cualquiera es de la forma: $z=a+bi$ ; donde “$a$” es la parte real de z y el número real “$b$” se llama la parte imaginaria de z.

Por ahora veremos dos formas de escribir un número complejo:

Forma Binomial: a+bi   y como Par Ordenado: (a,b)

Algunos números complejos pueden ser reales e imaginarios a la vez. Por ejemplo:

2.2 ¿Qué pasa con el 0?
Es un número complejo cuya parte real e imaginaria son 0;
Si un número tiene su parte imaginaria es 0 significa que es un número real, luego, el 0 es un numero real, imaginario y complejo.

2.3 Representación de un número complejo.

Un número complejo cualquiera lo denotaremos como $z=a+bi$ ; donde ya dijimos que:
a es la parte real y se anota: $Re\left(z\right)=a$ y b es la parte imaginaria y lo anotaremos$Im\left(z\right)=b$

Esto significa que el eje X corresponde a los números reales y el eje Y corresponde a la parte imaginaria.

Ejercitemos un poco: Completaremos en rojo la siguiente tabla:

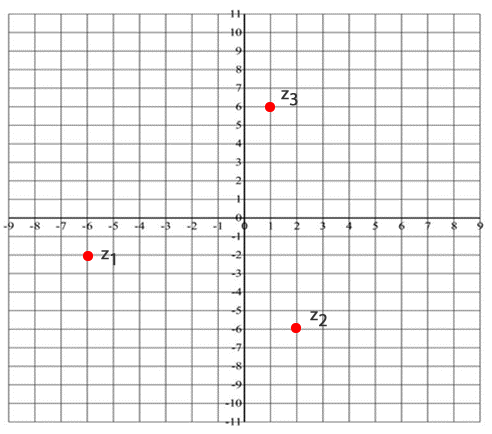
Como vimos anteriormente, una forma de escribir un número complejo es como par ordenado, por lo que se pueden representar en el plano cartesiano, ya que el eje X corresponde a la parte real e Y corresponde a la parte imaginaria:

Ejercicio: Escribe en forma binomial y luego representa cada número complejo en el plano cartesiano

a)$z_1=–6–2i=(–6,–2)$
b) $z_2=2–6i=(2,–6)$
c) $z_3=1+6i=(1,6)$

2.4 Igualdad de números complejos

Dos números son iguales cuando tienen sus partes reales e imaginarias iguales, esto es:

$z_1=a+bi$  y  $z_2=c+di$ ,donde $a,b,c,d\in \mathrm{ℝ}\Rightarrow z_1=z_2\iff a=c$y $b=d$

Ejemplos:
1.- Determina el valor de a para que $z_1:a+5i=z_2:3+5i$

Aquí:

$z_1=z_2\iff a=3$

2.- Determina los valores de a y b para que $z_1:–7+ai=z_2:b–1i$

Aquí:

$z_1=z_2\iff b=–7$ y $a=–1$