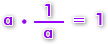1- Multiplicación y división de números racionales
Para multiplicar y dividir números racionales se puede utilizar su representación fraccionaria o decimal, igual como los has estudiado en cursos anteriores.
Para multiplicar o dividir números decimales infinitos periódicos o semiperiódicos por otro número racional, debes transformarlos a fracción, y los números mixtos transformarlos a fracción impropia.
Ejemplos:
a) Transforma el siguiente número decimal infinito periódico a fracción:
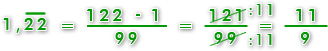
b) Transforma el siguiente número decimal infinito semiperiódico a fracción:
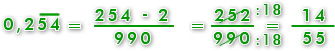
c) Transforma el siguiente número mixto a fracción impropia:
Debes aplicar al igual que para los números enteros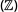 
la regla de los signos.
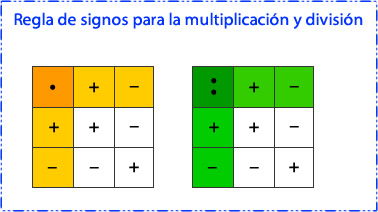
1.1- Multiplicación de fracciones
Para multiplicar fracciones, se multiplican los numeradores con los numeradores y los denominadores con los denominadores. Luego si es necesario se simplifica la fracción resultante. Siendo a,b,c,d diferentes de cero, pertenecientes al conjunto de los números enteros, lo podemos representar de la siguiente forma;
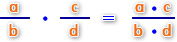
Ejemplos:
Recuerda siempre usar la regla de signos, en este ejercicio el resultado es negativo (-).
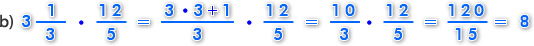
Para resolver este ejercicio, primero transformamos el número mixto a fracción impropia y luego multiplicamos.
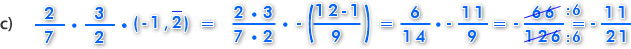
Para resolver este ejercicio, multiplicamos las 2 primeras fracciones y transformamos el decimal infinito periódico a fracción y luego, multiplicamos esta fracción por la fracción resultante de la primera multiplicación. Como el decimal es negativo y las fracciones positivas el resultado es negativo (-).
1.2- División de fracciones
Para dividir 2 fracciones, debes multiplicar la primera fracción por el inverso multiplicativo de la segunda fracción. Siendo a,b,c,d diferentes de cero, pertenecientes al conjunto de los números enteros, se puede representar de la siguiente forma;
Ejemplos:
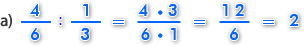
En este ejemplo puedes ver como invertimos la segunda fracción y luego multiplicamos por la primera fracción.
Para dividir estos números racionales, primeros transformamos el número mixto a fracción impropia, invertimos la segunda fracción y luego, multiplicamos las fracciones.
c)
38:-4:-0,3¯=-3·18·4:-3 :39 :3=-332:-13=-332·-31=932
Para resolver este ejercicio, invertimos el número – 4 (sabiendo que -4 = -4/1) y lo multiplicamos por la primera fracción. Además, transformamos el decimal infinito periódico a fracción común (lo que dio como resultado -3/9) y simplificamos (1/3), luego invertimos la fracción (-3/1), y multiplicamos por el resultado de la división de las 2 primeras fracciones.
1.3- Propiedades de la multiplicación y la división en los números racionales
En la multiplicación de números racionales se cumplen las propiedades de clausura, asociativa, conmutativa, distributiva, elemento neutro y elemento inverso.
Sean a, b, c, d diferentes de 0.
a) Clausura:
Si multiplicamos o dividimos dos números racionales, el resultado será siempre un número racional. Por lo tanto, el conjunto de números racionales es cerrado para la multiplicación y para la división.
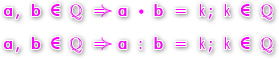
b) Asociativa:
Independiente de como se agrupen los números racionales dentro de la multiplicación, el resultado será el mismo.
c) Conmutativa:
Puede variar el orden de los números racionales en la multiplicación y el resultado será el mismo. Donde se puede ocupar la frase “el orden de los factores no altera el producto”.
d) Distributiva:
Al combinar sumas y multiplicaciones, el resultado es igual a la suma de los factores multiplicado por cada uno de los sumandos.
e) Sacar factor común:
Es el proceso inverso a la propiedad distributiva. Si varios sumandos tienen un factor común, podemos extraer dicho factor, y escribirlo como el producto de la suma de los otros factores.
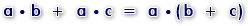
f) Elemento neutro:
En la multiplicación y la división de números racionales, existe un elemento neutro que es el número uno, cuyo producto o cociente con otro número racional, dará como resultado el mismo número.
g) Elemento inverso multiplicativo:
El inverso de un número racional en la multiplicación, dará como resultado el número uno.
