1- Método de completar el cuadrado para resolver la ecuación de 2° grado o cuadrática de la forma
El método de completar el cuadrado, también llamado completación de cuadrado, o compleción de cuadrados, es la técnica que se utiliza cuando tenemos una ecuación de segundo grado o cuadrática, del tipo , con a distinto de 0, y la transformamos, primero en un trinomio cuadrado perfecto, con el fin de “completar” la ecuación para crear un cuadrado de binomio y así poder despejar la incógnita X y llegar a las raíces o soluciones.
Para que puedas entender mejor este método, consideraremos primero la ecuación del tipo , la cual, si transponemos el término nos queda; .
Si observamos la primera parte de la igualdad vemos que tenemos el binomio , al cual le falta un término para formar un trinomio cuadrado perfecto (¿?)2. Este término es el cuadrado de la mitad del coeficiente del segundo término, , si resolvemos el cuadrado quedaría .
Lo graficaremos para que puedas entender mejor;
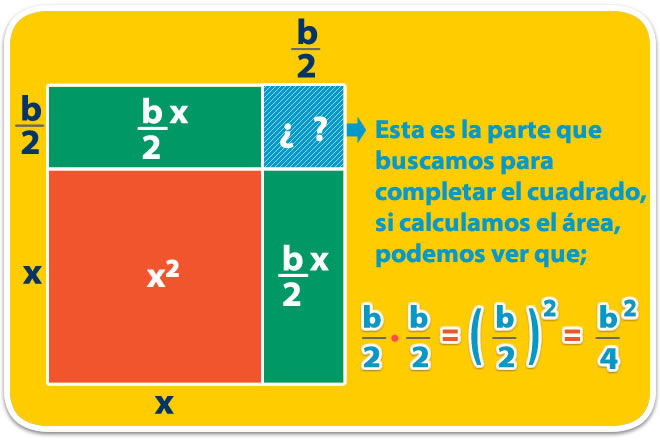
Entonces, formamos así el trinomio cuadrado perfecto; cuyo primer término es el cuadrado de x, su segundo término es el doble del producto de por y su tercer término es el cuadrado de la mitad de . Para que no se altere la ecuación, agregamos la misma cantidad al otro lado de la igualdad.
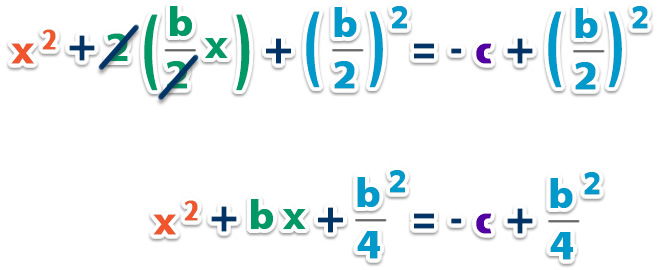
– Factorizamos el trinomio cuadrado perfecto;
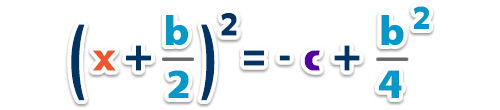
– Extraemos la raíz cuadrada a ambos lados de la igualdad para quitar el cuadrado;
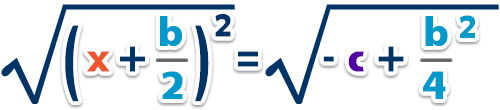
– Ordenamos y pasamos al otro lado de la igualdad;
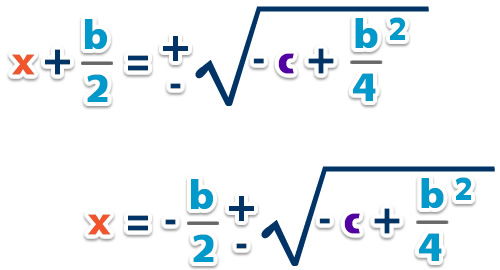
– Entonces, las raíces de la ecuación son;
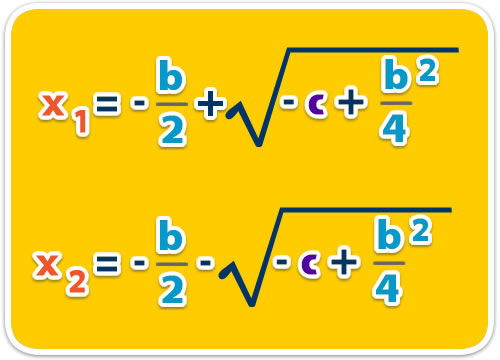
– Ahora que ya entendiste este método, veamos cuando el coeficiente a de es mayor que 1. El procedimiento es esencialmente el mismo, solo que antes dividimos por a la ecuación.
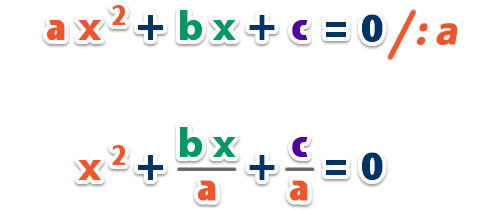
– Y realizamos los mismos pasos ya explicados; Transponemos el término independiente y agregamos el término que falta para lograr el trinomio cuadrado perfecto (que es la mitad de al cuadrado) en ambos lados de la igualdad;
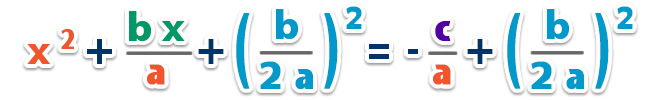
– Factorizamos el trinomio cuadrado perfecto;
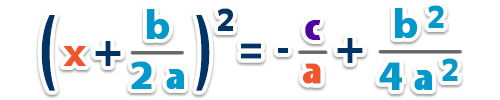
– Extraemos la raíz cuadrada a ambos lados de la igualdad para quitar el cuadrado;
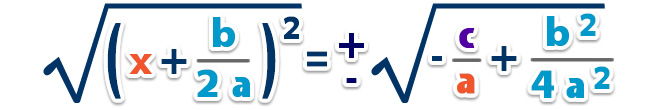
– Ordenamos y pasamos al otro lado de la igualdad;
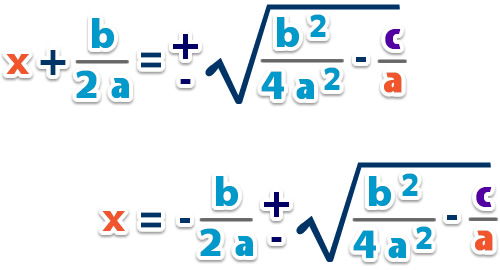
– Entonces, las raíces de la ecuación son;
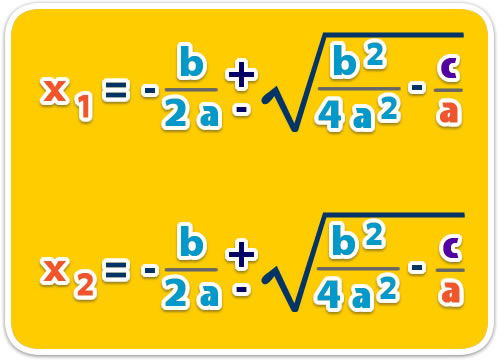
Si siguiéramos desarrollando la ecuación que obtuvimos por método de completar el cuadrado, también llegaríamos a la fórmula general, explicada en el tema anterior. Veamos
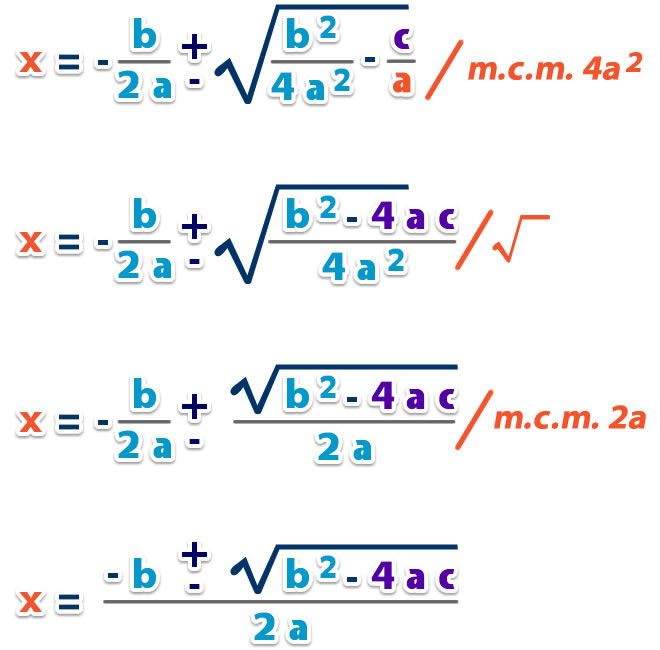
Con esto se demuestra que el método para llegar a las raíces de la ecuación de segundo grado es el mismo en ambos casos, la diferencia está en que por el método de completar el cuadrado tienes que realizar todo el desarrollo, en cambio, al aplicar la fórmula general solo es necesario reemplazar los datos.
Ejemplos:
a) Resuelve por método de completar el cuadrado la ecuación x2 = 16 x – 63.
– Primero ordenaremos la ecuación;
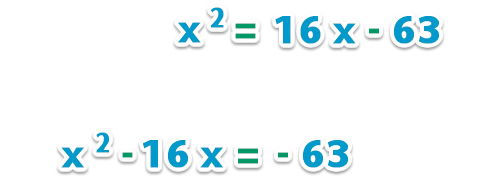
– Agregamos el término a ambos lados de la igualdad para formar el trinomio cuadrado perfecto (recuerda que es el cuadrado de la mitad del cociente x);
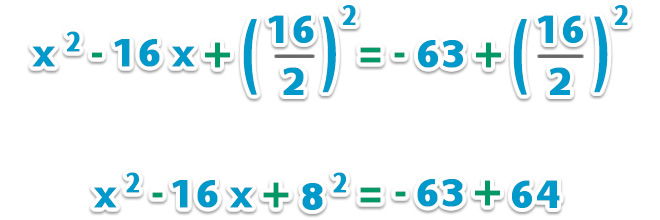
– Factorizamos el trinomio cuadrado perfecto;

– Extraemos la raíz cuadrada a ambos lados de la igualdad para quitar el cuadrado;
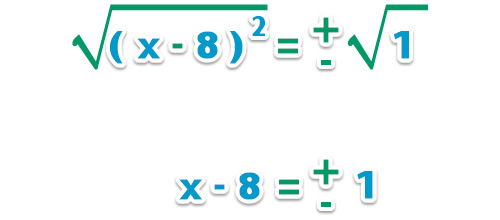
– Pasamos – 8 al otro lado de la igualdad y resolvemos las raíces de la ecuación;
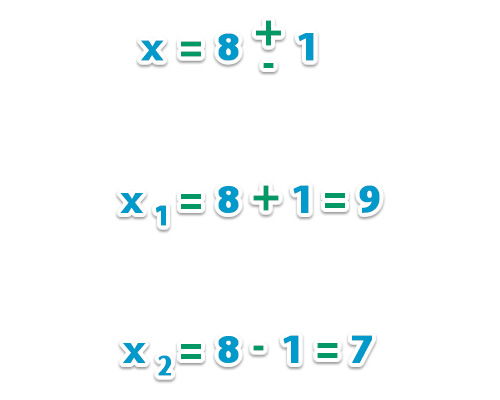
Respuesta: Las raíces de la ecuación son 7 y 9.
b) Resuelve por método de completar el cuadrado la ecuación 3x2 – 5 x + 2 = 0.
– Primero, como el cociente de es mayor que 1, dividimos la ecuación por esta cantidad (3) y transponemos el término independiente;
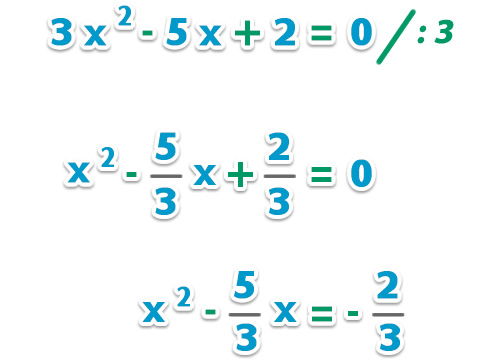
– Agregamos el término a ambos lados de la igualdad para formar el trinomio cuadrado perfecto (recuerda que es el cuadrado de la mitad del cociente de x);

– Factorizamos el trinomio cuadrado perfecto;
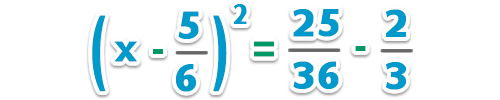
– Extraemos la raíz cuadrada a ambos lados de la igualdad para quitar el cuadrado y resolvemos;
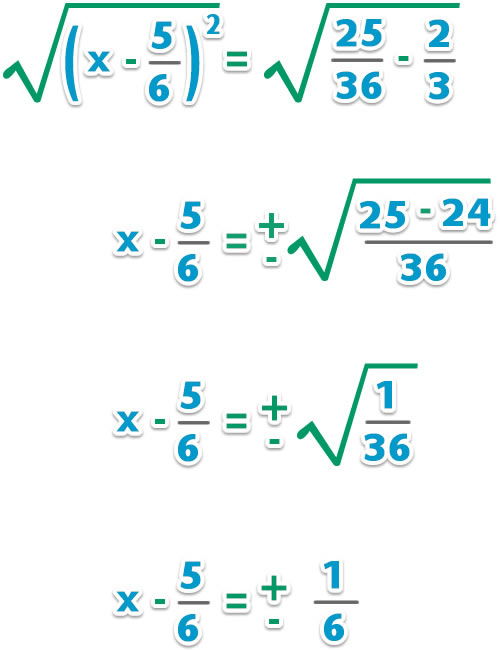
– Pasamos al otro lado de la igualdad y resolvemos las raíces de la ecuación;
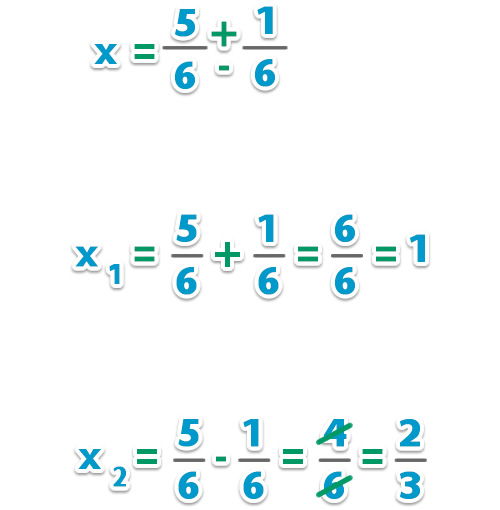
Respuesta: Las raíces de la ecuación son y .

