1- Tablas de frecuencia
Una tabla de frecuencia resume la información acerca de la cantidad de veces que una variable toma un valor determinado. Además, permite organizar e interpretar de manera más rápida y eficiente.
1.1- La frecuencia absoluta
Corresponde a la cantidad de veces que se repite un dato. Denotamos este valor por fi.
La suma de las frecuencias absolutas es igual al número total de datos, que se representa por N.
Por Ejemplo:
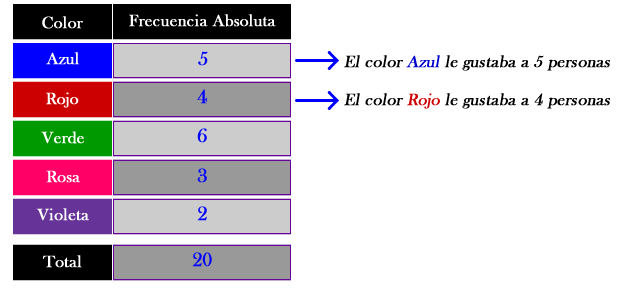
Si hacemos una encuesta a 20 personas para saber cuál es su color favorito obtenemos lo siguiente:
[Tabla 1]
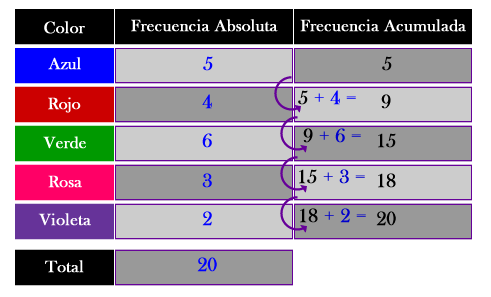
1.2- La Frecuencia Absoluta Acumulada
Se obtiene sumando sucesivamente las frecuencias absolutas. Denotamos este valor por Fi.
[Tabla 2]
1.3- La Frecuencia Relativa
Es la probabilidad de obtener cierto dato, se obtiene calculando la razón entre la frecuencia absoluta de un dato con el total. Se puede expresar como fracción, decimal o porcentaje. Denotamos este valor por hi.
[Tabla3]
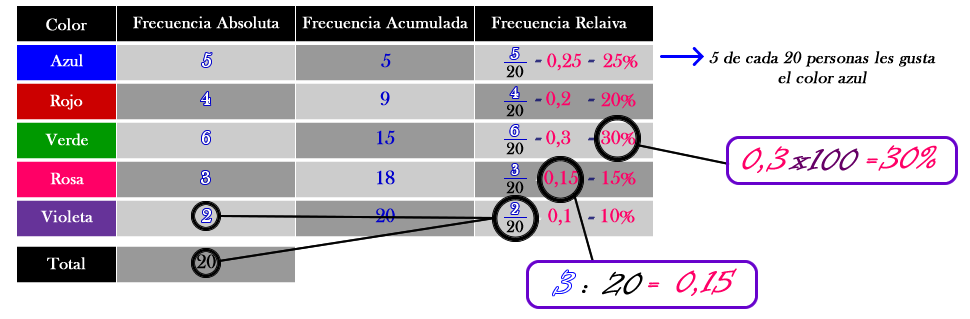
Para obtener el numero en decimal se divide la frecuencia absoluta por el total y para obtener el porcentaje se multiplica este decimal por 100.
Los ejemplos representan una tabla de frecuencias de datos No agrupados, en el caso de las tablas de datos Agrupados representan las frecuencias en rangos de datos, como en el siguiente caso.
Se entrevistan a 28 personas que realizan un taller preguntándoles la edad que tengan:
[tabla 4]
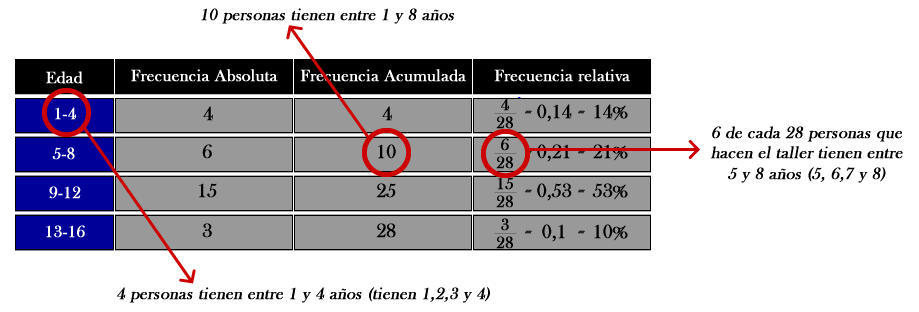
1.4- Frecuencia relativa acumulada
La frecuencia relativa acumulada es el cociente entre la frecuencia acumulada de un determinado valor y el número total de datos. Se puede expresar en tantos por ciento. Denotamos este valor por Hi
Se calcula:
Fi /N
2- Interpretar tablas de frecuencia
Veamos la siguiente situación:
Se realizó una encuesta los estudiantes de un séptimo básico para conocer la cantidad de hermanos que tienen.
Los resultados obtenidos fueron los siguientes:
1 – 2 – 0 – 1 – 0 – 2 – 3 –2 –1 – 0 – 1 – 0 –1 – 2 – 4 – 3 – 1– 2 – 4 – 3
¿Cómo ordenar y representar los datos en una tabla de frecuencia?
Paso 1: Ordenar y clasificar los datos.
Se clasifican los datos según el número de hermanos que tengan los estudiantes, para diferenciar un dato de otro se pueden emplear diferentes colores.
1 – 2 – 0 – 1 – 0 – 2 – 3 –2 –1 – 0 – 1 – 0 –1 – 2 – 4 – 3 – 1– 2 – 4 – 3
0 hermanos = 4 estudiantes.
1 hermano = 6 estudiantes.
2 hermanos = 5 estudiantes.
3 hermanos = 3 estudiantes.
4 hermanos = 2 estudiantes.
Paso 2: Registrar la frecuencia absoluta y frecuencia absoluta acumulada en una tabla.
La frecuencia absoluta (fi) indica cuántas veces se repite cada dato, por ejemplo, 6 estudiantes afirmaron que tienen 1 hermano.
La sumatoria de la frecuencia absoluta debe ser equivalente con la cantidad de datos obtenidos, en este caso, se encuestaron a 20 estudiantes.
N = 20
La frecuencia absoluta acumulada (Fi) es el resultado de sumar sucesivamente las frecuencias absolutas. La suma debe dar como resultado el valor de N, en este caso, 20.
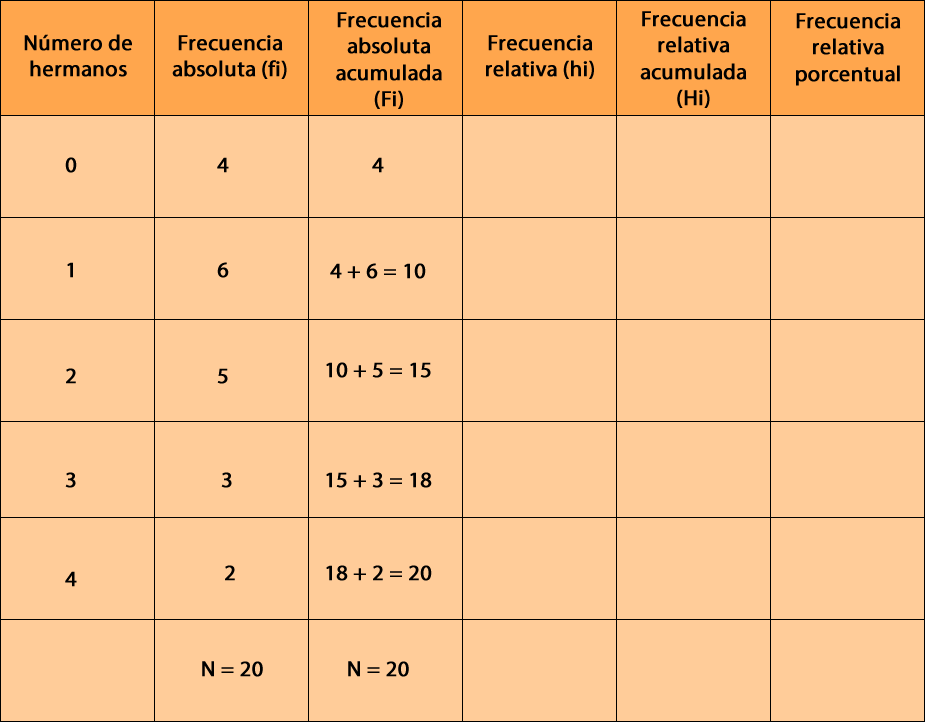
Paso 3: Registrar la frecuencia relativa y frecuencia relativa acumulada en la tabla.
Recuerda que la frecuencia relativa (hi) se puede expresar como fracción o decimal. Corresponde al cociente entre la frecuencia absoluta y el tamaño total de la muestra.
La frecuencia relativa acumulada (Hi) se obtiene al sumar sucesivamente las frecuencias relativas. La suma debe dar como resultado 1.

Paso 4: Calcular la frecuencia relativa porcentual.
La frecuencia relativa porcentual expresa la frecuencia relativa como porcentaje. Para calcularla se multiplica la frecuencia relativa por 100.
Por ejemplo, para conocer el porcentaje asociado a los estudiantes que no tienen hermanos se puede multiplicar 0,2 por 100 obteniendo el 20%.
La sumatoria de todos los porcentajes debe ser igual a 100%.
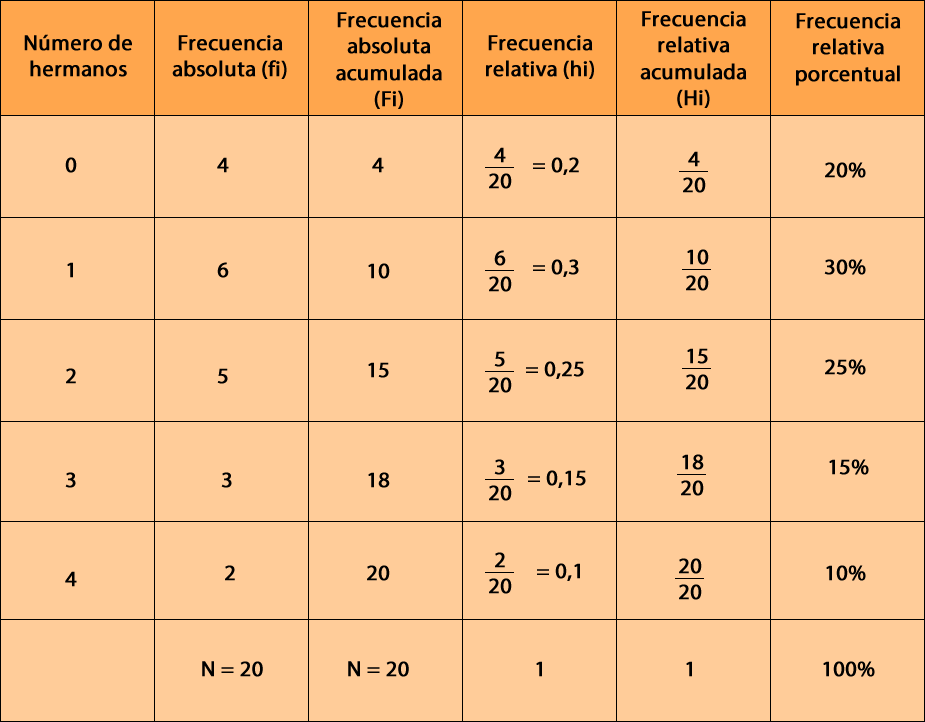
2.1- Interpretemos la tabla de frecuencia
A partir de la tabla de frecuencia, podemos decir lo siguiente:
– 20 personas fueron encuestadas. → se observa la frecuencia absoluta acumulada o se suman los datos presentados en la columna frecuencia absoluta.
– 4 estudiantes encuestados no tienen hermano. → se observa la frecuencia absoluta de 0 hermanos.
– 2 estudiantes encuestados tienen 4 hermanos. → se observa la frecuencia absoluta de 4 hermanos.
– 5 estudiantes encuestados tienen más de 2 hermanos. → se suman las frecuencias absolutas de 3 y 4 hermanos.
– El 30% de los estudiantes encuestados tiene un hermano. → se observa el porcentaje asociado a 1 hermano.
– El 50% de los encuestados tiene más de 1 hermano. → se observa el porcentaje asociado a 2, 3 y 4 hermanos, sumando los porcentajes.
¿Qué otras conclusiones puedes extraer a partir de la tabla?
2.2- Situación 2
La siguiente tabla de frecuencia muestra la cantidad de mascotas que tiene un grupo de personas, sin embargo, está incompleta. ¿Qué valores tienen A, B y C?
|
Número de mascotas |
Frecuencia absoluta |
Frecuencia absoluta acumulada (Fi) |
Frecuencia relativa (hi) |
Frecuencia relativa acumulada (Hi) |
Frecuencia relativa porcentual |
|
0 |
8 |
8 |
8/40 |
8/40 |
20% |
|
1 |
12 |
20 |
12/40 |
20/40 |
30% |
|
2 |
A |
36 |
16/40 |
36/40 |
C |
|
3 |
4 |
40 |
B |
40/40 |
10% |
Valor de A:
Una forma de resolverlo es observando las filas de frecuencia absoluta y frecuencia absoluta acumulada, luego determinamos qué número sumado a 20 da 36.
36 – 20 = 16
Valor de B:
Recuerda que la frecuencia relativa corresponde al cociente entre la frecuencia absoluta y el tamaño total de la muestra.
Observamos la frecuencia absoluta asociada a 3 mascotas y es igual a 4. El total de la muestra es 40, por lo que se puede expresar como 4/40.
Valor de C:
Una forma de resolverlo es multiplicando la frecuencia relativa asociado a 2 mascotas por 100.
1640=0,40,4 ·100 = 40%
También se puede observar cuánto falta para completar el 100% en la columna frecuencia relativa porcentual.

