1- Introducción
En este tema estudiaremos sobre el exponente de función potencia, ¿qué significa?, cómo es su gráfica y sus propiedades.
La función potencia es aquella función que está compuesta de la siguiente manera:
| y |
2- Analizando las gráficas
Se puede observar una diferencia en la gráfica de la función potencia cuando tiene exponente par, impar negativo o positivo:
Exponente par positivo:
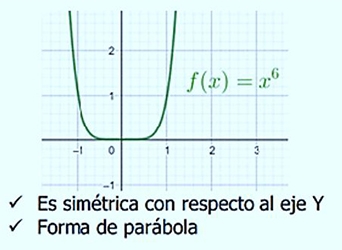
Exponente impar positivo:
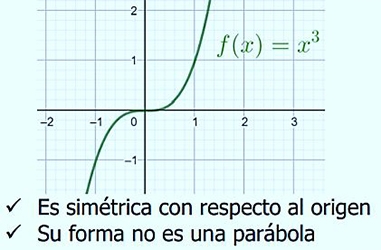
Además de analizar la forma gráfica de la función considerando los exponentes, es necesario analizar cuando el coeficiente numérico “” es positivo o negativo (no puede ser cero, ya que no existiría función potencia).
Además de analizar la forma gráfica de la función considerando los exponentes, es necesario analizar cuando el coeficiente numérico es positivo o negativo (no puede ser cero, ya que no existiría función potencia).
Exponente par positivo:
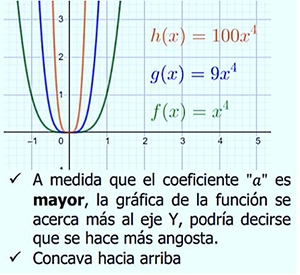
Exponente impar positivo:
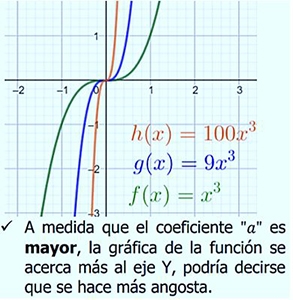
Ahora veremos las gráficas cuando “” es negativo:
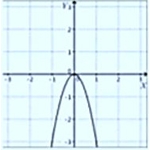
Exponente par positivo:
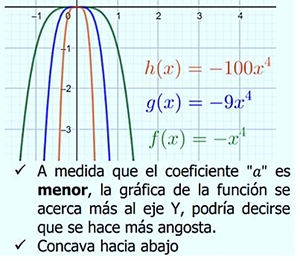
Exponente impar positivo:
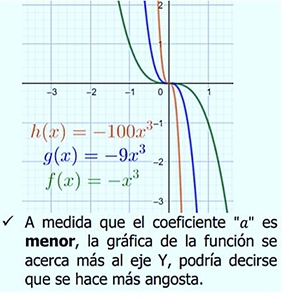
Ejemplos:
Observemos que, si el exponente “n” es un número entero positivo, no hay restricciones para los valores que puede tomar x en la función potencia, o sea, la función está definida para todos los números reales, luego . En cambio, para determinar el recorrido de la función, es necesario distinguir qué pasa en los casos cuando “n” es par o impar.
Las siguientes gráficas corresponden a la Función Potencia, donde el exponente es par positivo:
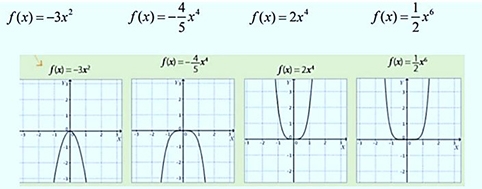
El recorrido de esta función serán los números reales positivos (incluyendo el cero) cuando , y serán los números reales negativos (incluyendo el cero) cuando .
Las siguientes gráficas corresponden a la Función Potencia, donde el exponente es impar positivo:
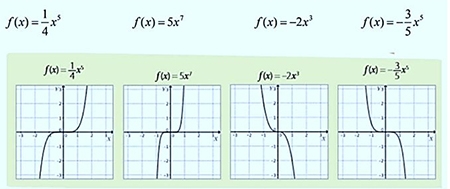
Si te fijas, los valores de y correspondientes a la función , para n impar positivo:
El Dominio de las gráficas es el conjunto de todos los números reales (mira siempre el eje X).
El Recorrido de las gráficas también es el conjunto de todos los números reales (mira siempre el eje Y).
Si el gráfico ocupa el I y III Cuadrante. La función siempre es Creciente.
Si el gráfico ocupa el II y IV Cuadrante. La función siempre es Decreciente.
Resumiendo:
| n > 0 | ||
| n Impar | 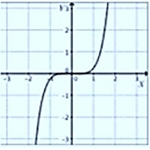 |
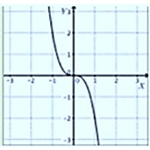 |
| n Par | 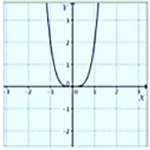 |
 |

