1- Función exponencial
Una función exponencial, es una función de la forma donde “a” es una constante positiva distinta de 1 y x es cualquier número dentro de los reales, es decir:
El dominio de la función exponencial son los números reales. En cambio, el recorrido son solo los reales positivos. Hay que recordar que el dominio son los valores que puede tomar la variable independiente, representada por “x”, y el recorrido son los valores que puede tomar la variable dependiente, representada por “y”.
De forma gráfica, se puede observar de la siguiente manera:
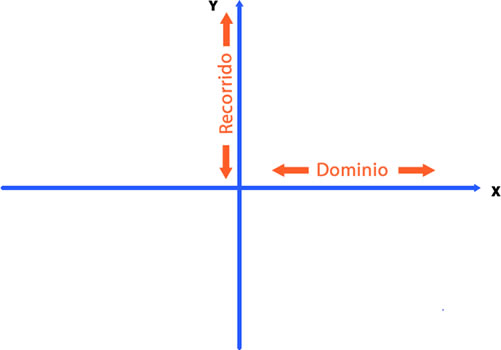
Nota: recordar que las funciones pueden ser representadas de distintas maneras (ej: , etc.) Además, de manera general, estas son representadas con la letra “Y”.
Propiedades:
a)
b)
c)
Demostración:
ya que
por propiedad,
d) Tiene como asíntota el eje X (es decir, nunca corta al eje x)
2- Gráfica de la función exponencial
Hay distintas maneras de graficar esta función. Esta dependerá de los valores que tome “a” en . Analizaremos cada caso.
a)
La gráfica de esta función es decreciente. Es decir, a medida aumentan los valores de X, disminuyen los valores de
.
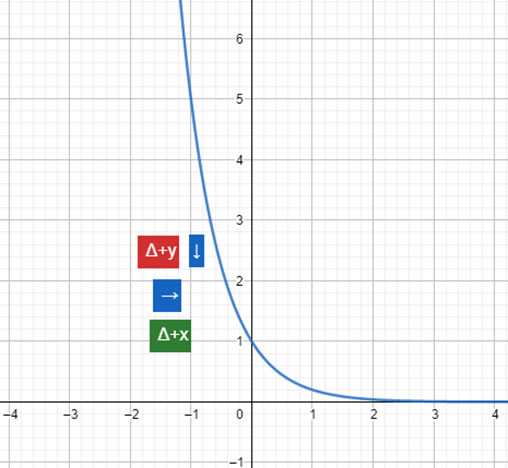
Ejemplos de funciones exponenciales decrecientes:
b)
La gráfica de esta función es creciente. Es decir, a medida aumentan los valores de X, aumentan los valores de
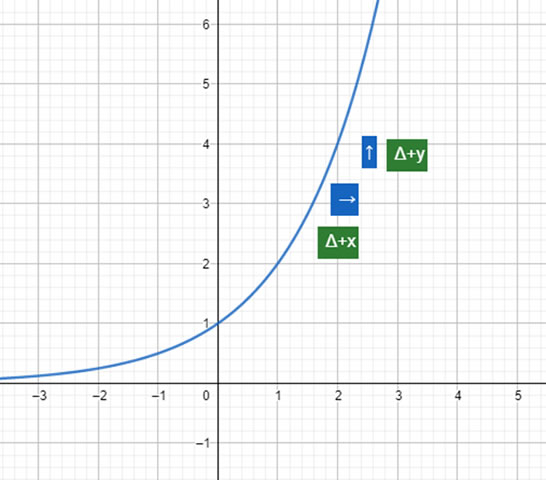
Ejemplos de funciones exponenciales crecientes:
Donde e es un numero irracional que vale aproximadamente 2,7183
Podemos notar que en el primer caso a medida disminuye X, la función va creciendo cada vez más rápido, es decir, aumenta cada vez más el valor de Y. En el segundo, es lo mismo, pero cuando X aumenta.
En los casos anteriores, sin ningún tipo de traslación o transformación, la gráfica de la función SIEMPRE corta al eje Y en el 1. Es decir, su intercepto con el eje Y se da en el punto (0,1).
Reemplazando
Por propiedad,
3- Función recíproca de
Para cualquier función exponencial de la forma, su función recíproca está dada por . Al momento de graficar, observamos que son simétricos con respecto al eje Y.
Ejemplo:
Sea ; sabemos que . Entonces, el recíproco de es
Gráficamente:

4- Traslaciones de la función exponencial
Los casos anteriormente mencionados tienen distintas variaciones que pueden resultar en un movimiento de la función en la gráfica, sin cambiar su forma. Con las traslaciones, cambian las propiedades mencionadas al principio.
a) Traslación horizontal
En este caso, la grafica se mueve a la izquierda o a la derecha, dependiendo del valor que tome “C” en la fórmula:
Traslación a la derecha.
Traslación a la izquierda.
Gráficamente podemos ver:

Observamos que, en la traslación horizontal, el corte con el eje Y cambia según el valor de la constante c.
Sea una función exponencial con traslación horizontal:
Este ejemplo es válido para cualquier “c” distinto de 0. En el caso de que “c” sea cero, ya no sería una traslación.
Ejemplo: Determine el intercepto con el eje Y de la función
El corte con el eje Y se da cuando el valor de x es igual a cero. Es decir, debemos evaluar la función en x=0.
El intercepto con el eje y de esta función es en el punto (0,16). Gráficamente:

b) Traslación vertical
En este caso, la función es trasladada hacia arriba o hacia abajo, según el valor que tome la constante “K”.
Traslación hacia arriba.
Traslación hacia abajo
Gráficamente:
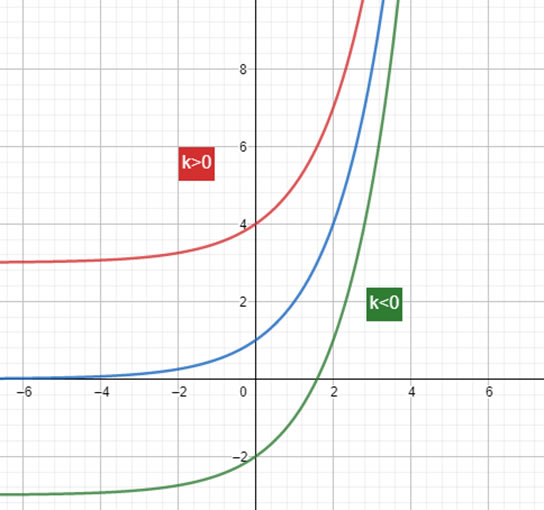
El corte con el eje Y cambia según el valor de la constante k.
Además, las traslaciones verticales cambian el recorrido de la función. Antes, el recorrido de la función exponencial eran los números reales positivos (). Ahora, aplicando la traslación vertical, son los números reales mayores a “k” ().
Ejemplo:
Sea la función . Determine el intercepto con el eje Y. Además, determine el recorrido de la función.
Solución:
Reemplazando x=0 en la función, tenemos que:
Entonces, la función corta al eje Y en el punto (0,0).
Con respecto al recorrido, sabemos que son todos los reales mayores a “k”. Es decir, todos los reales mayores a -1.
Gráficamente:

Importante: Si se aplica tanto una traslación horizontal como una vertical, el intercepto en el eje Y sería
Ejemplos:
1) Sea la función. Determine la o las traslaciones, su dominio y recorrido.
Solución:
Observamos que la función tiene una constante sumando en el exponente. Esta representa una traslación horizontal de 2 unidades a la izquierda. Además, observamos que tiene otra constante restando fuera del exponente. Esta representa una traslación vertical de 4 unidades hacia abajo.
El dominio de esta función son todos los reales, ya que las traslaciones NO modifican el dominio. En cambio, el recorrido cambia debido a la traslación vertical. En este caso, el recorrido son todos los reales mayores a -4.
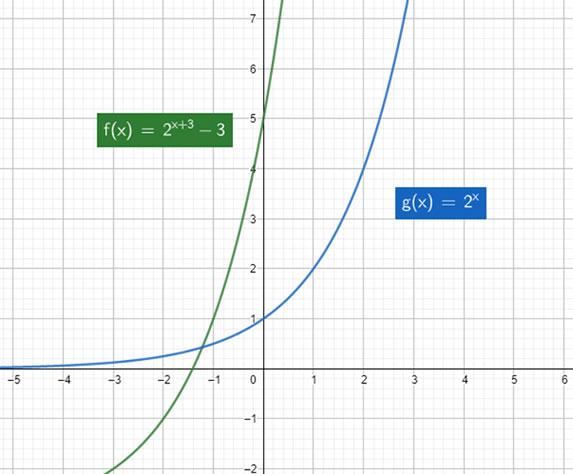
2) Sea la función representada con color verde. Identifique en el gráfico las funciones; ;

Solución:
Podemos notar que hay dos traslaciones horizontales y una traslación vertical. En este caso, podemos notar que la única función que tiene valores negativos en el eje Y es la función azul. Es decir, esta tuvo una modificación en su recorrido. Como sabemos, la traslación vertical es la única que cambia el recorrido de la función, por lo tanto, la función azul corresponde a .
Luego, notamos que hay una traslación horizontal hacia la derecha (naranja) y hacia la izquierda (roja). Siguiendo lo aprendido en el contenido, concluimos que corresponde a la función y a la función , respectivamente.
3) Observando el gráfico, determine cual es cada función.

Solución:
De todas las funciones, observamos que hay una que es decreciente (verde). Esta corresponde a la función que cumpla que . Entonces, la función verde es .
Luego, vemos tres funciones crecientes, las cuales gráficamente son muy similares. Para poder determinar cuál corresponde a cada una, debemos analizar cuál es la que tiene un mayor crecimiento exponencial. Hay que recordar que, en las funciones crecientes, a medida que el valor de “a” es mayor, mayor es su crecimiento exponencial.
Observando la gráfica, notamos que cuando “x” es negativo, la curva roja tiene un mayor valor de “y” que el resto de las funciones, lo cual podría hacernos pensar que es la que tiene un mayor crecimiento exponencial. Sin embargo, observamos que cuando “x” es positivo esta relación se invierte, es decir, es la que tiene un menor valor de “y”. En este caso, a nosotros nos importará el que sea mayor cuando “x” sea positivo.
Entonces, para Identificar la función con mayor crecimiento, debemos ver cual es la función que tiene un mayor valor de “y” para cualquier “x” positivo. Si por ejemplo observamos el valor de x cuando es 0,5 vemos que la curva roja toma aproximadamente un valor de 1,5 en el eje “Y”; la curva azul un valor de 1,7 y la curva naranja un valor de 2. Vemos que 1,5<1,7<2
Entonces, la función con mayor crecimiento exponencial es la naranja, luego la azul y por último la roja. Estas funciones corresponden a , respectivamente.
Desafío
El profesor de matemática dice lo siguiente: “Estoy buscando una función exponencial de base 2 que tenga una traslación horizontal de 3 unidades a la izquierda y un intercepto de 5”. Encuentre la función
Solución:
Empecemos escribiendo una función general.
Sabemos que la traslación horizontal se representa con la constante “C”. En este caso, como se mueve 3 unidades a la izquierda, sabemos que .
Para saber el valor de K, debemos saber el valor de la función cuando X es igual a cero.
Como sabemos que el intercepto debe ser igual a 5, entonces:
Por lo tanto, la función es:
Gráficamente, comparando con la función original: