1- Representar fracciones en la recta numérica
Para ubicar fracciones en la recta numérica se divide la unidad (entero) en segmentos iguales, como indica el denominador, y se ubica la fracción según indica el numerador.
Ejemplo de fracciones unitarias (con numerador 1) en la recta numérica:
a. Ubicar la fracción
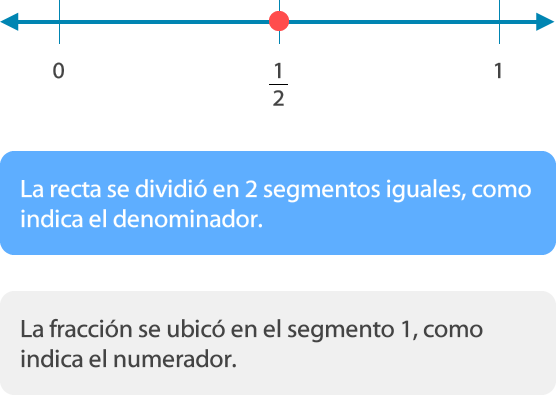
b. Ubicar la fracción

Como puedes observar las fracciones unitarias se ubican en el primer segmento de la recta numérica.
¿Cómo ubicar fracciones que no son unitarias?
Para ubicar fracciones que no son unitarias en la recta numérica se realiza el mismo procedimiento anterior, es decir, se divide el entero en partes iguales según lo que indique el denominador de la fracción. Luego, se ubica la fracción en el segmento que está señalado en el numerador.
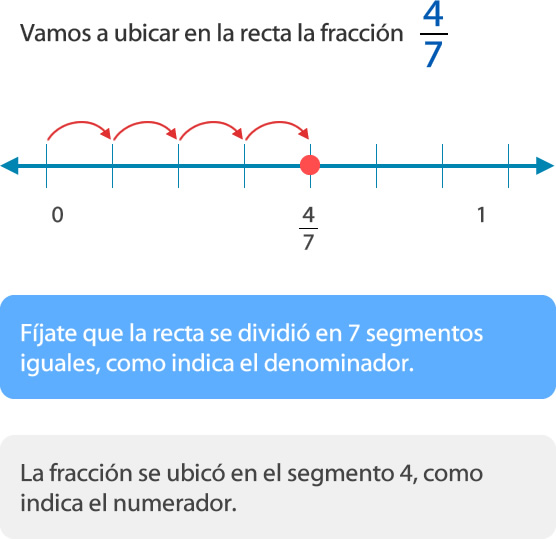
Recuerda que en la recta numérica el mayor de dos números es el que está más a la derecha.
2- ¿Cómo representamos en la recta numérica fracciones con distinto denominador?
Representaremos:
1.° Dividimos la recta de 0 a 1 en tantos intervalos como nos indique el producto de los denominadores de las fracciones. En este caso serán 6 intervalos, ya que 2 • 3 = 6
2.° Ubicamos ambas fracciones en la recta:
Para ubicar multiplicamos su numerados por el denominador de la otra fracción:
Entonces consideramos 3 de los intervalos de la recta.
Para ubicar multiplicamos su numerador por el denominador de la otra fracción:
Entonces consideramos 4 de los intervalos de la recta.
Aplicando los pasos anteriores, tenemos:

Para ubicar fracciones con diferente denominador también se puede realizar mediante una cuadrícula.
Ubicar las fracciones en una cuadrícula.
1.° Calcular el mínimo común múltiplo de los denominadores 4 , 2 y 5.
– Los múltiplos de un número se obtienen multiplicando dicho número por cualquier otro número natural.
– El mínimo común múltiplo de dos o más números corresponde al menor de los múltiplos comunes.
Para calcular el mínimo común múltiplo se puede realizar una lista con los primeros múltiplos de los números. Es decir, multiplicamos por 1, 2, 3, 4, etc.
Múltiplos de 2 = 2, 4, 6, 8, 10, 12, 14, 16, 18, 20…
Múltiplos de 4= 4, 8, 12, 16, 20, 24, 28, 32, 36, 40…
Múltiplos de 5 = 5, 10, 15, 20, 25, 30, 35, 40, 45, 50…
El primer múltiplo en común corresponde al mínimo común múltiplo, en este caso es 20.
2.° Trazar una recta marcando el 0 o punto de origen.

3.° Se divide en el entero según lo que indica el mínimo común múltiplo, es decir, en 20 partes iguales.

4.° Cuando cuentes 20 partes, marca en la recta el número 1 que representa un entero.

5.° Divide el número 20 por las cifras de los denominadores.
Por lo tanto, se cuenta 5 espacios comenzando desde cero.

Se cuentan 4 espacios comenzando desde cero.


Finalmente las fracciones quedan ubicadas de la siguiente manera:

3- Fracciones impropias en la recta numérica
Representaremos la fracción 5/3 en la recta numérica:
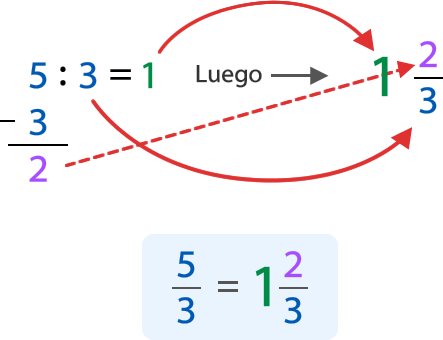
El entero 1 nos indica que la fracción está entre el 1 y el 2. Por eso, ubicaremos la fracción original en ese segmento de la recta (del 1 al 2).