Factorización

1- Factorización

Factorizar una expresión algebraica (o suma de términos algebraicos), es el procedimiento que permite escribir como multiplicación dicha expresión.

Los factores o divisores de una expresión algebraica son los términos, ya sean  números y/o letras, que multiplicados entre sí dan como producto la primera expresión.

Así, por ejemplo, si multiplicamos a por a + b podemos ver qué;

Dan como producto

a2 + ab

, entonces, los factores o divisores de esta expresión algebraica son a y

a + b

.

2- Métodos utilizados para factorizar un polinomio. 

Primero debes saber que, no todos los polinomios se pueden factorizar, ya que, al igual que en los números primos que sólo son divisibles por ellos mismos y por 1, hay expresiones algebraicas que también solo son divisibles por ellas mismas y por 1.

Por ejemplo, el polinomio

ax + by + cz

, no se puede factorizar ya que, solo es divisible por

ax + by + cz

y por 1. Es decir, este polinomio no tiene un factor en común.

Para poder factorizar una expresión algebraica es necesario que siempre exista  al menos un factor en común dentro de sus términos, ya sean números y/o letras.

Factor común de una expresión algebraica es el máximo común divisor (m.c.d.) de los términos que la componen.

2.1- Factor común monomio.

Debes identificar el factor común entre todos los términos de la expresión, y escribirlo como coeficiente de un paréntesis, en el cual tienes que escribir los términos resultantes después de dividir por el factor común.

Ejemplos:

a) Factorizar x²y + x²z.

Identificamos el factor común de x²y y x²z el cual es x², entonces dividimos los términos de la expresión por x²; x²y : x² = y  y   x² z : x² = z. Ahora escribimos la factorización;

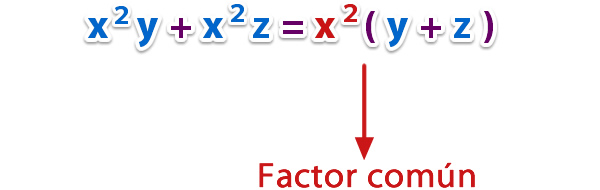
b) Factorizar 8 m² – 12 mn.

Identificamos el factor común de 8 m² y 12 mn el cual es 4m, entonces dividimos los términos de la expresión por 4m; 8 m² : 4m = 2m y 12 mn : 4m = 3n. Ahora escribimos la factorización;

2.2- Factor Común polinomio o por agrupación de términos

Cuando en una expresión algebraica, no todos los términos tienen algún factor en común, puedes realizar una agrupación en paréntesis de los términos que, si tienen, y así podrás factorizar.

Generalmente la agrupación puede hacerse de varios modos, lo importante es que siempre los términos que se agrupen tengan algún factor en común. Independiente de cómo se agrupen los términos, el resultado será el mismo.

Ejemplos;

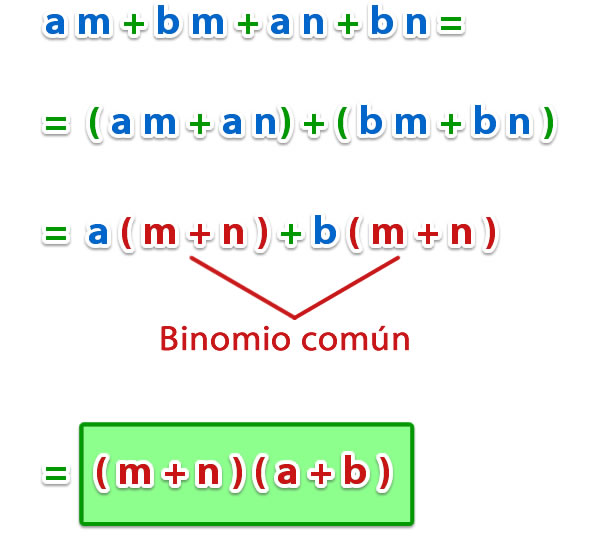
a) Factorizar la expresión a m + b m + a n + b n.

Podemos ver que, los dos primeros términos tienen el factor común m y los dos últimos el factor común n. Agrupamos los dos primeros términos en un paréntesis y los dos últimos en otro, precedido de un signo +, ya que es el signo del tercer término. Luego sacamos el factor común de cada paréntesis, y nos queda el binomio  en común (a + b), que se anota como producto de (m + n).

En este mismo ejemplo, podemos agrupar el primer y el tercer término que tienen el factor común

a

, y el segundo y cuarto término que tienen el factor común

b

, sacamos el factor común de los paréntesis y nos queda el binomio en común

(m + n)

, que se anota como producto de

(a + b)

.

 Nos da el mismo resultado, ya que el orden de los factores no altera el producto.

b) Factorizar la expresión 6 m – 9 n + 21 n x – 14 m x

Agrupamos los términos 1 y 2 que tienen factor común 3 y los términos 3 y 4 que tienen el factor común 7 x.

Como puedes ver, en el ejemplo anterior, los binomios

(2 m – 3 n)

y

(3 n – 2 m)

, no son exactamente iguales, por lo cual, para igualarlos, cambiamos el signo al segundo binomio y queda

(- 3 n + 2m)

, pero para que el producto

7 x (3 n – 2 m)

no variara, también le cambiamos el signo al factor

7 x

, convirtiéndolo en

– 7 x

.

En el ejemplo anterior, también podemos agrupar el primer y cuarto término, que tienen el factor común 2 m, y el segundo y tercer término que tienen el factor común 3 n. Fíjate que al agrupar en paréntesis, el segundo y tercer término, que son – 9 n y + 21 n x, lo anotamos como – (9 n – 21 n x), esto para que mantengan los signos de la expresión original.

Obtenemos el mismo resultado, ya que el orden de los factores no altera el producto.

2.3- Factorización de productos notables:

Para factorizar de forma más rápida una expresión algebraica  que cumpla con las condiciones, puedes utilizar productos notables.

a) Trinomio cuadrado perfecto

El trinomio cuadrado perfecto es igual al producto notable cuadrado de binomio o sea, es producto de dos binomios iguales:

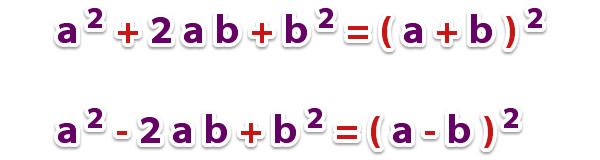
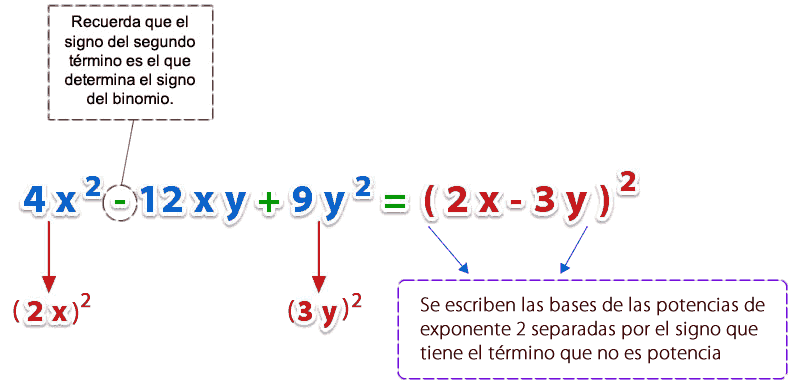
La regla para factorizar un trinomio cuadrado perfecto es; extraer la raíz cuadrada al primer y tercer término, y separar estas raíces por el signo del segundo término. Entonces, el binomio formado se eleva al cuadrado o se multiplica por sí mismo.

Ejemplo:

– Factorizar 4 x² – 12 x y + 9 y²

b) Diferencia de cuadrados

La diferencia de cuadrados perfectos es igual al producto notable suma por su diferencia;

La regla para factorizar una diferencia de cuadrados es; extraer la raíz cuadrada al primer y al segundo cuadrado, y se multiplica la suma de estas raíces cuadradas por su diferencia.

Ejemplo:

Factorizar 25 – 36 x²

c) Cubo de binomio

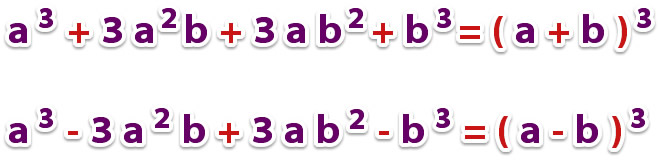
Si analizamos esta fórmula, para factorizar y llegar al producto notable cubo de binomio, es necesario que la expresión algebraica ordenada con respecto a una letra cumpla con las siguientes condiciones;

– Debe tener cuatro términos.

–  El primer y último término tienen que ser cubos perfectos.

–  El segundo término tiene que ser (sumado o restado) el triplo del  cuadrado de la raíz cubica del primer término multiplicado por la raíz cúbica del último término.

–  El tercer término tiene que ser sumado el triplo de la raíz cúbica del primer término por el cuadrado de la raíz cúbica del último término.

Si todos los términos de la expresión son positivos, es el cubo de la suma de las raíces cúbicas del primer y último término, y si los  términos son alternativamente positivos y negativos, la factorización será el cubo de la diferencia de dichas raíces.

Ejemplo:

Factorizar a³ + 3 a² + 3 a + 1.

Veamos si la expresión cumple con las condiciones para ser un cubo de binomio;

– La expresión si tiene 4 términos.

– El primer y último término, si son cubos perfectos.

– Como la raíz cubica de a³ es a, y la raíz cubica de 1 es 1, reemplazamos estos valores en la ecuación para comprobar si el segundo y tercer término corresponden;

Segundo término: 3 (a)² (1) = 3 a².

Tercer término: 3 (a) (1)² = 3 a.

Como puedes ver, la expresión algebraica cumple con todas las condiciones, y como todos sus términos son positivos, la factorización es el cubo de la suma de a y 1;

d) Suma de cubos.

La fórmula nos dice que, para factorizar la suma de dos términos elevados al cubo, se descompone en dos factores, donde;

– El primer factor, es la suma de sus raíces cúbicas.

– El segundo factor, es el cuadrado de la primera raíz, menos el producto de las dos raíces, más el cuadrado de la segunda raíz.

Ejemplo:

Factorizar a³ + 27.

– La raíz cubica de a³ es a, y de 27 es 3.

– Según la fórmula sería, (a + 3) (a² – a (3) + (3)²)

e) Diferencia de cubos.

La fórmula nos dice que, para factorizar la diferencia de dos términos elevados al cubo, se descompone en dos factores, donde;

– El primer factor, es la diferencia de sus raíces cúbicas.

– El segundo factor, es el cuadrado de la primera raíz, más el producto de las dos raíces, más el cuadrado de la segunda raíz.

Ejemplo:

Factorizar x³ – 125.

– La raíz cubica de x³ es x, y de 125 es 5.

– Según la fórmula sería, (x – 5) (x² + x (5) + (5)²)

f) Trinomio de la forma x² + bx + c.

Los trinomios ordenados de la forma

x2 + bx + c

, corresponden al producto de dos binomios que tienen un término en común.

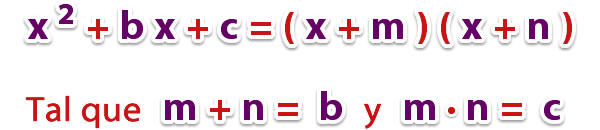
Para que aprendas a reconocer este tipo de trinomio, te tienes que fijar que cumpla las siguientes condiciones;

– El coeficiente del primer término es 1.

– El primer término es una potencia con exponente 2, generalmente su base es una letra.

– El segundo término tiene la base de la potencia del primer término y su coeficiente es una cantidad cualquiera, positiva o negativa y se obtiene al sumar o restar los términos no comunes y multiplicar ese resultado por el término común.

– El tercer término es independiente de la letra que aparece en el primer y segundo término, y es una cantidad cualquiera, positiva o negativa y se obtiene al multiplicar los términos no comunes.

Para que aprendas como anotar los signos de los binomios, y entiendas más este tipo de factorización te mostramos los siguientes ejemplos;

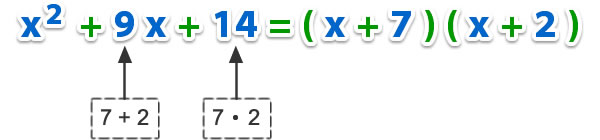
1) Factorizar x² + 9 x + 14.

El trinomio se descompone en dos binomios, donde el primer término de ellos será la raíz cuadrada de x², o sea x, ya que x es el término común en ambos paréntesis.

Cuando el segundo y tercer término del trinomio son positivos, ambos binomios tendrán signo positivo.

Los segundos términos de los binomios serán dos números que sumados den 9 y multiplicados den 14.

2) Factorizar y² – 8y + 15.

El trinomio se descompone en dos binomios, donde el primer término de ellos será la raíz cuadrada de y², o sea y,ya que y es el término común en los paréntesis.

Cuando el segundo término del trinomio es negativo y tercer término positivo, ambos binomios tendrán signo negativo.

Los segundos términos de los binomios serán dos números que sumados den – 8 y multiplicados den 15.

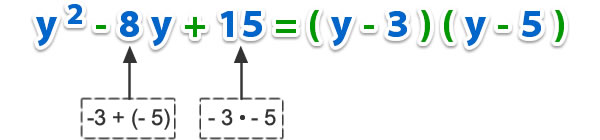
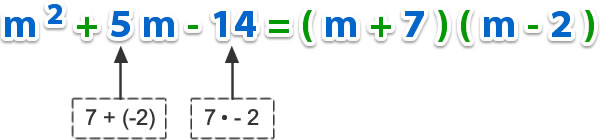
3) Factorizar m² + 5m -14.

El trinomio se descompone en dos binomios, donde el primer término de ellos será la raíz cuadrada de m², o sea m, ya que m es el término común en ambos paréntesis.

Cuando el segundo término del trinomio es positivo y tercer término negativo, los binomios tendrán signos distintos, donde el número de mayor valor absoluto será positivo.

Los segundos términos de los binomios serán dos números que sumados den 5 y multiplicados den – 14.

4) Factorizar a² – 2a – 15.

El trinomio se descompone en dos binomios, donde el primer término de ellos será la raíz cuadrada de a², o sea a, ya que a es el término común en ambos paréntesis.

Cuando el segundo y tercer término del trinomio son negativos, los binomios tendrán signos distintos, donde el número de mayor valor absoluto será negativo.

Los segundos términos de los binomios serán dos números que sumados den – 2 y multiplicados den – 15.

2.4- Trinomio de la forma ax² + bx + c

Se diferencian de los trinomios estudiados en el caso anterior, en que el primer término tiene por coeficiente un número distinto de 1.

Para factorizar este tipo de trinomios, tienes que multiplicar el trinomio por el coeficiente de x², dejando solamente indicado el producto del segundo término, luego puedes factorizar como aprendiste en el caso anterior, y por último tienes que dividir por el mismo número que multiplicaste.

Ejemplo;

Factorizar 20 x² + 7x – 6.

Multiplicamos el trinomio por el coeficiente de x² que es 20 y dejamos solamente indicado el producto de 20 por 7 x, nos queda;

Pero

400 x2 = (20x)2 y 20 (7x) = 7 (20x)

, podemos escribir el trinomio de la siguiente forma;

Ahora, factorizamos como aprendiste en el caso anterior, repasemos;

El trinomio se descompone en dos binomios, donde el primer término de ellos será la raíz cuadrada de

(20 x)2

, o sea

20 x

, pues

20x

será el término común en ambos paréntesis.

Cuando el segundo término del trinomio es positivo y tercer término negativo, los binomios tendrán signos distintos, donde el número de mayor valor absoluto será positivo.

Los segundos términos de los binomios serán dos números que sumados den 7 y multiplicados den – 120.

Para cancelar la multiplicación por 20, tenemos que dividir por 20, para esto sacamos el factor común de cada binomio y dividimos;

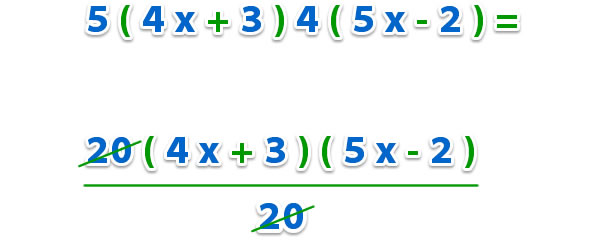
Respuesta: 20 x² + 7x – 6 = (4x + 3) (5x – 2).