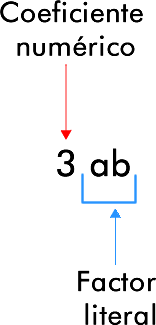
1- Término algebraico
Corresponde al producto de una constante numérica y una literal.
2- Expresiones algebraicas
Una expresión algebraica se forma al mezclar los términos algebraicos con las operatorias de suma o resta.
Por ejemplo:
2x+4y
, en este caso tenemos dos términos algebraicos y la operación de suma, al juntar estas tres cosas se forma la expresión algebraica
2x+4y
Si tenemos
2xy
, en este caso solo tenemos un término algebraico que a su vez también es una expresión algebraica. Ya que:
2xy=xy+xy
3- Lenguaje algebraico
Corresponde a expresar números y operaciones matemáticas utilizando expresiones algebraicas.
Ejemplo 1:
Exprese el enunciado “el triple de un número” algebraicamente.
Solución:
El enunciado habla de un número ¿Conocemos ese número? este número es desconocido, por lo tanto, lo expresaremos con la incógnita “x”.
Asumiremos que el número es “x”, como nos pide el triple de ese número, entonces solo debemos multiplicarlo por tres. Quedando:
3x→
el triple de un número
Ejemplo 2:
Redacte un enunciado que exprese
2x+5
Solución:
En este caso lo tenemos al revés.
Como sabemos la incógnita “x” representa un número que no conocemos delante de ese número hay un 2 que está multiplicando, entonces tenemos el doble de un número.
Para terminar, hay un 5 positivo. Quedando:
“El doble de un número aumentado en 5”.
4- Clasificación expresiones algebraicas
Las expresiones algebraicas se pueden clasificar respecto al número de términos algebraicos que las componen:
a) Monomios:
Son expresiones algebraicas que solo tienen un término algebraico. Por ejemplo:
5x; 4y; 3z; 2xy
b) Binomios:
Son expresiones algebraicas que tienen dos términos algebraicos y una operación de suma o resta. Por ejemplo:
2x+3y 5xy-2zy
c) Trinomios:
Son expresiones algebraicas que tienen tres términos algebraicos y dos operaciones de suma y/o resta. Por ejemplo:
2x+3y-2z 5xy+2zx-xy
Nota: Si la expresión algebraica tiene cuatro o más términos, hablamos de polinomios. (El término polinomio se puede usar en forma general para cualquier expresión algebraica).
5- Reducción de términos semejantes
Se llaman términos semejantes a todos aquellos términos que tienen igual factor literal, es decir, a aquellos términos que tienen iguales letras (símbolos literales) e iguales exponentes.
Ejemplo: 2mn y -8mn
Son términos semejantes porque ambos tienen en común el factor literal mn
Reducir términos semejantes significa sumar o restar los coeficientes numéricos en una expresión algebraica, que tengan el mismo factor literal.
Ejemplos:
x + 4x = 5 x 11b + 9 b = 20b 15m – 5m = 10 m -30x + 12x = -18x
Nota: dos términos semejantes con igual coeficiente y distinto signo se anulan.
5.1 Reducción de un polinomio que contenga términos semejantes de diversas clases
Para reducir un polinomio con diversos términos semejantes de diversas clases, se procede de la siguiente manera:
1- Se agrupan los términos semejantes de cada clase en un mismo paréntesis.
2- Se reducen los términos semejantes.
3- Se da la respuesta, ordenando el polinomio resultante.
Nota:
Recordemos que los términos semejantes son aquellos que tienen las mismas letras y afectadas por los mismos exponentes.
Ejemplos:
a) -81x + 19y – 30z + 6y + 80x + x – 25y
Agrupamos los términos semejantes:
(-81x + 80x + x ) + (19y+ 6y– 25y) – 30z
Reducimos términos semejantes (sumamos o restamos) y damos la respuesta.
0x + 0y -30z = -30z
b) -6m + 8n +5 –m –n -6m -11
1° Se agrupan términos semejantes
(-6m –m -6m) + ( 8n –n) + (5 – 11)
2° Reducimos términos semejantes (sumamos o restamos)
(-13m) + (7n) + (-6)
3°Se da la respuesta, ordenando el polinomio resultante.
-13m + 7n – 6
1.2- Términos entre paréntesis
Los paréntesis más usados son:
{ } = Llaves
[ ] = Corchetes
( )= Redondos
Si encuentras ejercicios donde se presentan paréntesis dentro de otro paréntesis, estas expresiones se resuelven de adentro hacia fuera.
Al reducir términos semejantes que estén expresados entre paréntesis se debe considerar lo siguiente:
⇒ Si un paréntesis es precedido por un signo (+) este se suprime sin variar los signos de los términos que están dentro del paréntesis.
Ejemplo:
7a + (-3a + 5b) = 7a – 3a + 5b = 4a + 5b
⇒ Si un paréntesis es precedido por un signo negativo (-), este se suprime cambiando los signos de los terminos que están dentro del paréntesis.
Ejemplo:
12a – (4a – 6b) = 12a – 4a + 6b = 8a + 6b
⇒ Si un paréntesis está precedido por una multiplicación, se utiliza la propiedad distributiva de la multiplicación respecto de la adición, es decir el término que está multiplicando, lo hace por cada término que está dentro del paréntesis.
Ejemplo
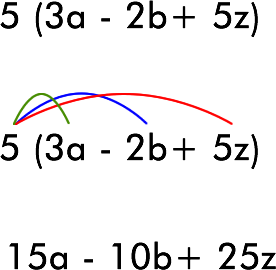
Ejercicios
Elimine paréntesis y reduzca términos semejantes:
a) (2a + 3b) + (4a – 7b)
b) (a + 2b) – (7a – 3b)
c) [ 12 – (3x +4) ] – [7 + (8 -9x)]
d) (3a -2b + 5c) – (-3b -5c -3a)
e) 3x +2y – [x – (x-y)]
f) 3y – 2z- 3x- {x- [y- (z-x)] – 2x}

