1- Fracciones en la vida diaria
En la vida cotidiana las personas utilizan diferentes expresiones en donde se utilizan fracciones, por ejemplo:

“Me comí la mitad de una barra de chocolate”.
Se refiere a que la persona dividió el chocolate en dos partes iguales y se comió una de ellas.

“Son las siete y cuarto”.
“y cuarto” se señala para indicar 15 minutos o la cuarta parte de una hora. Si se divide 60 por 4 resulta 15.

“La botella tiene una capacidad de medio litro”
Las expresiones medios y cuartos están relacionados con el concepto de fracción y como puedes ver en las situaciones anteriores, las fracciones son utilizadas para referirse a las partes de un objeto o para expresar unidades de medidas de tiempo, volumen, longitud, etc.
Te dejamos planteada la siguiente pregunta, ¿en qué otras situaciones de la vida diaria se utilizan fracciones?
1.1- Fracciones con material concreto
Para comprender de mejor manera qué es una fracción te invitamos a realizar la siguiente actividad.
Toma un papel lustre y dóblalo por la mitad como se muestra en la imagen.
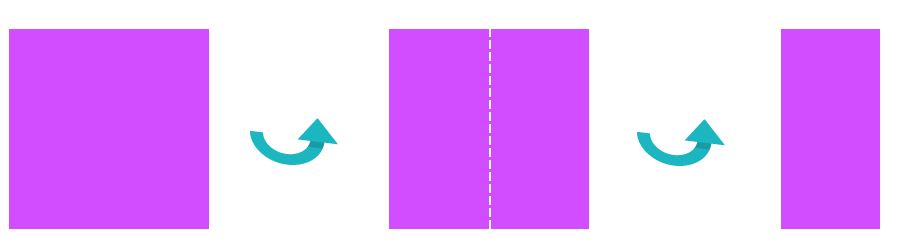
Desdobla el papel lustre y observa cuántas partes iguales hay. En total son dos partes iguales y cada una se denomina “un medio”.
A continuación, dobla nuevamente el papel como se indica en la imagen. ¿Cuántas partes iguales ves ahora?

Al desdoblar el papel puedes ver cuatro partes iguales, cada una de ellas corresponde a “un cuarto”, porque el papel se dividió en 4 partes iguales.
Utilizando el mismo papel lustre, dóblalo de manera diagonal como se señala en el ejemplo.
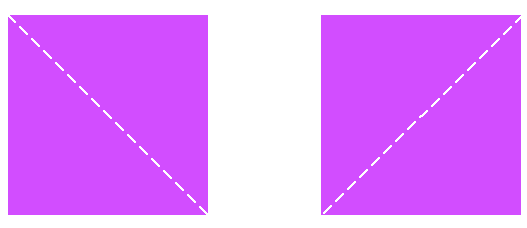
Desdobla por última vez el papel lustre, ¿cuántas partes iguales vez ahora?
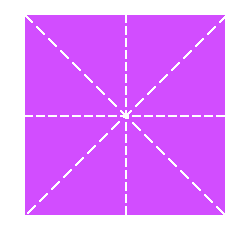
En total se ven 8 partes iguales, puedes comprobar cortando los trozos y poniéndolos unos sobre otros. Cada una de estas partes corresponde a “un octavo”, porque el papel se dividió en 8 partes iguales.
Como pudiste notar, las partes en las que se dividió el papel lustre en todos los casos son iguales, lo mismo ocurre con las fracciones.
2- Concepto de fracción
Una fracción representa las partes consideradas de un entero que ha sido dividido en partes iguales.
Las fracciones se representan matemáticamente por números que están escritos uno sobre otro y que se hallan separados por una línea recta horizontal llamada línea fraccionaria, que representa la operación de la división.
Una fracción está compuesta por un numerador y un denominador.

El numerador de la fracción, es el número de partes que se considera de la unidad o total.
El denominador, indica el número de partes en que se ha dividido la unidad.
Por ejemplo, cuando decimos una cuarta parte de un chocolate, estamos dividiendo el chocolate en cuatro partes y consideramos una de ellas.

3- Escritura y lectura de fracciones
Para leer fracciones, primero se nombra el numerador de la fracción y luego el denominador.
Las fracciones con denominadores entre 2 y 9 poseen nombres especiales:
2 = medios.
3 = tercios.
4 = cuartos.
5 = quintos.
6= sextos.
7 = séptimos.
8 = octavos.
9 = novenos.
Los denominadores 10 se denominan décimos y desde 11 en adelante se nombra el número y se agrega el sufijo “avos”.
En la tabla se muestran ejemplos de la lectura de fracciones:
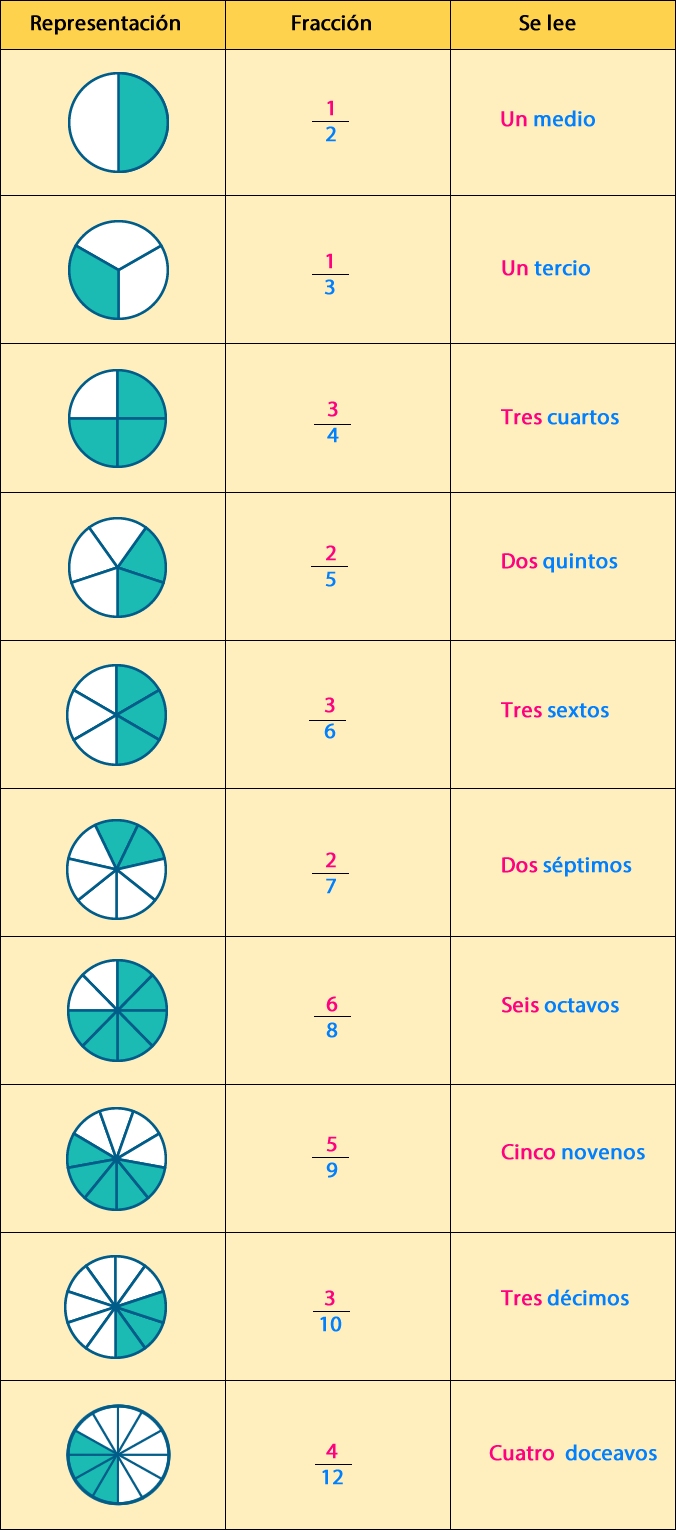
4- Representación de fracciones
4.1- Modelo de área
Se representan los enteros con figuras geométricas que se dividen en partes iguales. Las figuras que se utilizan para representar las fracciones pueden ser cuadrados, rectángulos, círculos, pentágonos, entre otros.
Ejemplo:
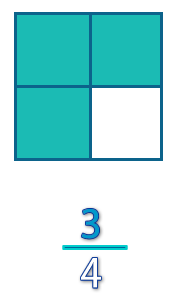
Para representar tres cuartos se dibujó un cuadrado y se dividió en 4 partes iguales de las cuales se consideraron 3.
4.2- Representación como conjunto
Consiste en una colección de elementos individuales. El denominador de la fracción indica la cantidad total de elementos y el numerador representa la cantidad de elementos que se consideran del conjunto.
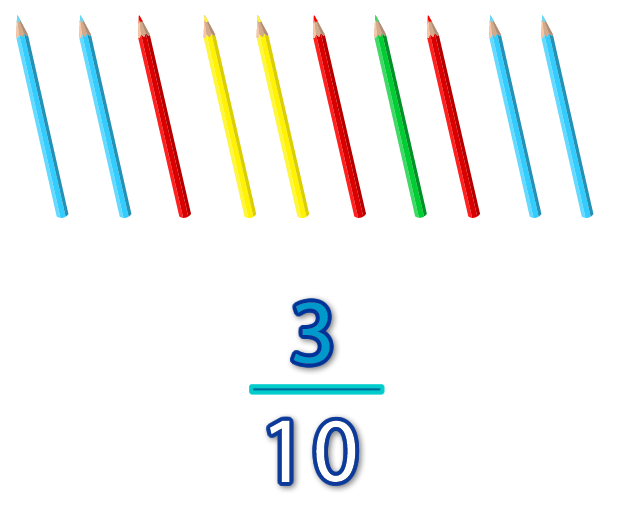
Ejemplo 1 : De un total de 10 lápices, 3 son de color rojo.
Matemáticamente se expresa el 3 en el numerador de la fracción y el número 10 en el denominador.
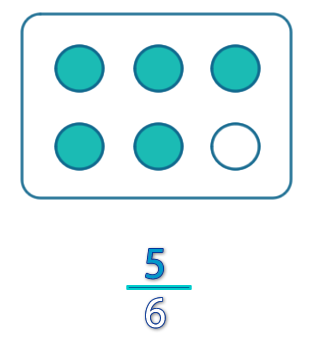
Ejemplo 2: De un total de 6 elementos se consideran 5.
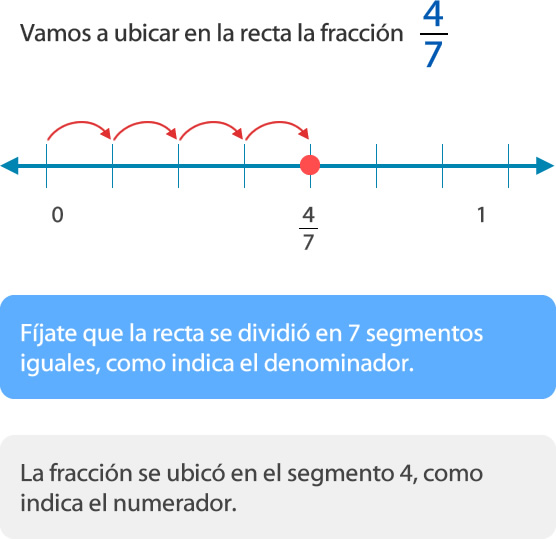
4.3- Recta numérica
Para representar fracciones en la recta numérica se divide la unidad (entero) en segmentos iguales, como indica el denominador, y se ubica la facción según indica el numerador.
Por ejemplo: