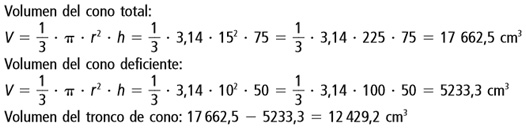1- ¿Qué es el cono?
El cono es un cuerpo geométrico generado por un triángulo rectángulo al girar en torno a uno de sus catetos.
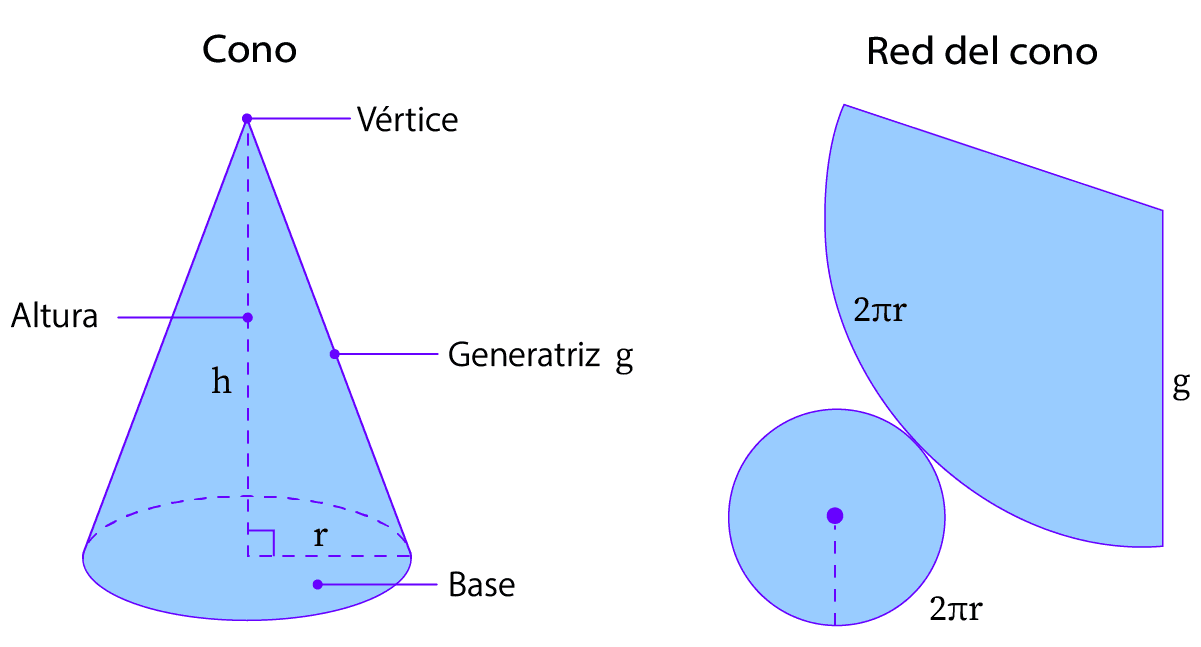
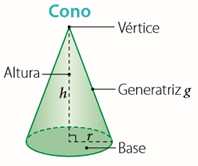
1.1- Elementos del cono
En el dibujo de arriba podemos distinguir los elementos de un cono recto:
– Eje: es el cateto AC. Alrededor de él gira el triángulo rectángulo ABC.
– Base: es el círculo que se genera producto de la rotación del otro cateto, AB. Por lo tanto AB es el radio del cono. La base se simboliza: O (A, AB).
– Generatriz: es la hipotenusa del triángulo rectángulo, BC, que genera la región lateral conocida como manto del cono.
– Altura: corresponde al eje del cono, porque une el centro del círculo con la cúspide siendo perpendicular a la base.
El cono tiene una cara basal plana y una cara lateral curva. Posee una arista basal y un vértice llamado cúspide.
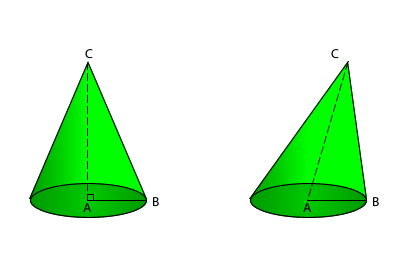
1.2- Tipos
Si la altura coincide con su eje, el cono es recto. Si el eje y la altura no coinciden, el cono es oblicuo.
1.3- Área de un cono
El área de un cono (A) puedes obtenerla al visualizar su red de construcción y la calculas utilizando:
Acono = Abase + Alateral
= π r2 + π r g
= π r (r + g)
Donde:
r es el radio de la base.
g la generatriz del cono.
Además, g2 = r2 + h2
Ejemplo:
Calcula el área del cono. Considera π ≈ 3,14.
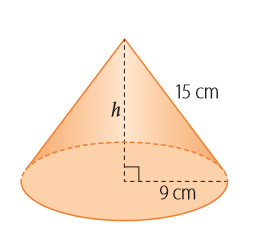
Al observar la imagen, se tiene que r = 9 cm y g = 15 cm.
Luego, al calcular el área, se tiene que:
A = π r (r + g)
A = π 9 (9 + 15) cm2
= π 9 (24) cm2
= 216 π cm2
= 678, 24 cm2
Respuesta: El área del cono es 678, 24 cm2
En el caso que se conozca el ángulo central del manto, su área lateral la calculamos con la fórmula del área de un sector circular:
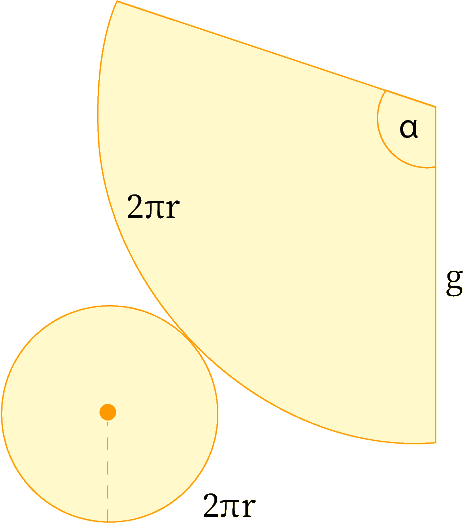
área lateral =
πr2α360°
Donde:
r = generatriz del cono.
Ejemplo:
Calcula el área de un cono de radio 3 y ángulo central del manto igual a 120°
Considerando:
Acono=Abase+Alateral
Obtendremos el área lateral usando la fórmula del área de sector circular :
π·r2·α360°
Se tiene
r = 3 cm
y
α=120°
, reemplazando:
Árealateral=π·r2·α360°Árealateral=π·32·120°360°Árealateral=π·9·120°360°Árealateral=π·93Árealateral=3πcm2
Obtendremos el área basal usando la fórmula del área del círculo
π·r2
Áreabasal=π·32Áreabasal=9πcm2
Finalmente, el área del cono será:
Acono=Abase+AlateralAcono=9π+3πAcono=12 π cm2
1.4- Cálculo del área del cono de generatriz desconocida
Para calcular el área (A) de un cono utilizas la expresión
A = π r (r + g)
Ejemplo: El radio mide 4 cm y la altura, 3 cm. Calcula la medida de la generatriz.
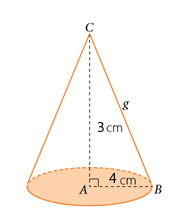
El radio r mide 4 cm, y la altura h mide 3 cm por lo que falta calcular la medida de la generatriz g. Para calcularla se utilizará el teorema de Pitágoras en el triángulo ABC.
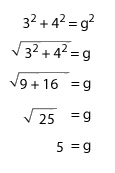
Luego, el área corresponde a:
A = 4 π (4 + 5) cm2 = 36 π cm2 y al considerar π ≈ 3,14, se tiene que es aproximadamente 113,04 cm2.
Respuesta: El área del cono es 36 π cm2 y al considerar π ≈ 3,14; se tiene que aproximadamente es: 113,04 cm2.
2- Volumen de un cono
El volumen (V) de un cono corresponde a un tercio del volumen de un cilindro con igual área de la base e igual medida de la altura.
Sea un cono de radio r y altura h, su volumen (V) se encuentra dado por la expresión:

Ejemplo1: Calcula el volumen de un cono si su altura mide 12 cm y su radio mide 5 cm.
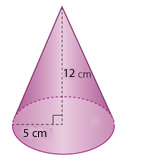
Al calcular el volumen del cono remplazas r = 5 cm y h = 12 cm en la expresión:
Vcono=13·πr2hVcono=13·π·52·12Vcono=13·25·12Vcono=13·300πcm3Vcono=100πcm3
Respuesta: El volumen del cono, es
100 π cm3
y considerando
π ≈ 3,14
, el volumen es aproximadamente
314 cm3
.
Ejemplo 2: Calcula el volumen de un cono si su generatriz mide 15 cm y su radio mide 9 cm.
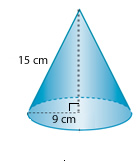
Al aplicar el teorema de Pitágoras para calcular la medida de la altura del cono, se tiene que:
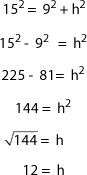
Luego, la medida de la altura del cono es 12 cm.
Al calcular el volumen del cono remplazas r = 9 cm y h = 12 cm en la expresión:
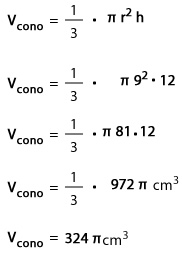
Respuesta: El volumen del cono, es 324 π cm3 y considerando π ≈ 3,14, el volumen es aproximadamente 1.017,36cm3.

El volumen (V) corresponde al espacio que ocupa un cuerpo. Algunas unidades de medida de volumen son:
– km3 (kilómetro cúbico)
– m3 (metro cúbico)
– cm3 (centímetro cúbico)
3- Volumen de un cono truncado
En el caso de un cono truncado, el volumen se puede calcular como la diferencia entre el volumen del cono, como si estuviera completo, y el cono menor que lo complementa, es decir:
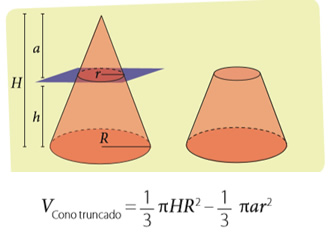
Utilizando el teorema de Thales, se puede demostrar que el volumen del cono truncado está dado por la expresión:

Donde R y r son los radios de las bases y h es la altura del cono truncado.
Ejemplo: Halla el volumen del tronco de cono.
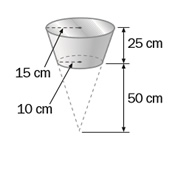
Desarrollo:
El volumen del tronco del cono viene dado por la diferencia del volumen del cono total y el cono deficiente.