1- ¿Qué es redondear un número?
Los números redondeados son más fáciles para cuando tienes que hacer cálculos mentales. Los números redondeados son solo aproximados. No puedes tener una respuesta exacta con números redondeados. Algunas veces no se necesita una respuesta exacta.
Ejemplo: 73 redondeado a la decena más cercana es 70, porque 73 está más cerca de 70 que de 80.

Al redondear, lo hacemos aproximando a los múltiplos de 10, 100, 1 000, 1 000 000, etc. que estén más cercanos, dependiendo de la exactitud que necesitamos que tengan nuestros datos.
2- Redondear a la centena más próxima
Para redondear números a la centena más próxima, convierte los números que terminan de 1 a 49 al número inferior más próximo que termina en 00. Por ejemplo, 424 redondeado a la centena más próxima sería 400.

Los números que tienen los dos últimos dígitos iguales o mayores a 50 deberán ser redondeados a la centena mayor más próxima. El número 988 redondeado a la centena más próxima será 1 000.

3- Cómo redondear números
Para redondear números primero debes ubicar o destacar la cifra que se encuentra en la posición solicitada, luego observa el dígito que está a su derecha:
– Si el dígito es menor que 5, la cifra que se encuentra en la posición destacada se conserva y los dígitos de la derecha se reemplazan por ceros.
– Si el dígito es mayor o igual que 5, se le suma 1 unidad a la cifra que se encuentra en la posición destacada y los dígitos de la derecha se reemplazan por ceros.
Veamos algunos ejemplos.
Ejemplo 1:
Redondear a la UM el número 345 678.
1.° Ubicas el dígito que se encuentra en la UM.

2.° Observas el dígito que se encuentra a la derecha de la cifra destacada. Debes fijarte si es menor, mayor o igual que 5.
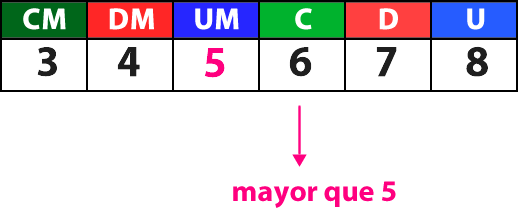
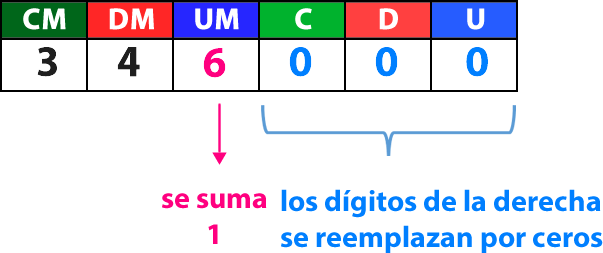
En este caso la cifra es mayor que 5, por lo tanto, al dígito destacado en la UM se le agrega una unidad y las cifras de la derecha se reemplazan por ceros.
Podemos comprobar utilizando la recta numérica:
Dibujamos el tramo que va desde 345 000 y 346 000, luego dividimos la recta en 10 partes iguales.
Determinamos la ubicación aproximada de 345 678.

345 678 se encuentra entre 345 000 y 346 000, y está más cercano a 346 000, por lo tanto, se aproxima a dicha cifra.
Ejemplo 2:
Redondear a la DM el número 234 598.
1.° Ubicas el dígito que se encuentra en la DM.

2.° Observas el dígito que se encuentra a la derecha de la cifra destacada. Debes fijarte si es menor, mayor o igual que 5.
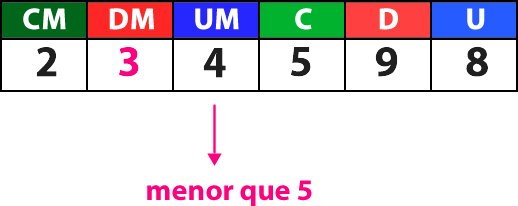
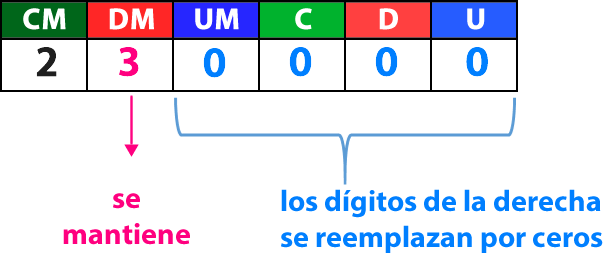
En este caso la cifra es menor que 5, por lo tanto, el dígito destacado en la DM se mantiene y las cifras de la derecha se reemplazan por ceros.
Podemos comprobar utilizando la recta numérica:
Dibujamos la recta desde va desde 230 000 hasta 240 000, luego dividimos la recta en 10 partes iguales:
Determinamos la ubicación aproximada de 234 598.

234 598 se encuentra entre 230 000 y 240 000, y está más cercano a 230 000, por lo tanto, se aproxima a dicha cifra.
3.1- Estimación de una suma por redondeo.
Una forma rápida de estimar la suma de dos números es redondeando cada número y luego sumando los números redondeados. Probablemente, este no sea el resultado exacto, pero puede ser, para algunos propósitos, lo suficientemente cercano.
Cómo estimar una suma por redondeo
– Redondea cada término que vas a sumar.
– Suma los números redondeados.
– Algunas veces una estimación se puede mejorar. Si estimamos la suma de 345 + 440, redondearíamos 345 en 300 y 440 en 400. La estimación sería 300 + 400 o 700. Ambos números fueron redondeados para abajo. El número 345 fue redondeado hacia abajo en 45 y 440 fue redondeado hacia abajo en 40. La suma de 45 + 40 da 85, que se redondea en 100. Entonces una mejor estimación sería 800. La suma real es 785.
Cómo mejorar la estimación
– Redondea cada término que vas a sumar.
– Suma los números redondeados.
– Si ambos son redondeados hacia arriba o hacia abajo, fíjate si la cantidad de redondeo es más que 50. De ser así, suma o resta 100 a la estimación.
– Si un número es redondeado hacia abajo y el otro es redondeado hacia arriba, no encontrarás una estimación más cercana utilizando este método.
Algunos usos del redondeo son:
Corroborar si se tiene dinero suficiente para comprar lo que uno quiere.
Tener una idea aproximada de la respuesta correcta a un problema.
Ejemplo 1:

¿Cuál es el precio aproximado del refrigerador y la cocina?
En este caso redondearemos los dos valores a la DM.
Refrigerador: 219 990 220 000
Cocina: 159 990 160 000
Luego, realizamos la suma:

Nota: El símbolo se usa para aproximar un número a otro.
El precio aproximado de los dos productos es $380 000.
Ejemplo 2:
Si redondeamos los datos de la suma a la unidad de millón más cercana, tenemos:

Luego el resultado exacto es: 16 315 960
Ejercicios
1) Redondea cada número a la unidad de millón más cercana y calcula el resultado aproximado. Luego con la ayuda de la calculadora obtén el resultado exacto.
a) 5 127 463 + 82 400 002
b) 77 375 760 + 4 220 500
c) 193 016 019 + 1 078 080
2) Felipe recorre 878 000 metros el primer día de su viaje y 297 000 metros el segundo día. ¿Cuál es la mejor estimación de los kilómetros totales recorridos por Felipe?
a) 1 000 km
b)1 100 km
c) 1 200 km
d) 1 400 km
3- Si redondeamos 8 247 406 a la decena de mil más próxima se obtiene:
a) 8 000 000
b) 8 250 000
c) 8 300 000
d) 8 500 000
Respuestas:
1- a) 87 000 000 ; 87 527 465
b) 81 000 000 ; 81 596 260
c) 194 000 000 ; 194 094 099
2- c
3- b

