1- Círculo y Circunferencia
1.1- ¿Qué diferencia tienen?
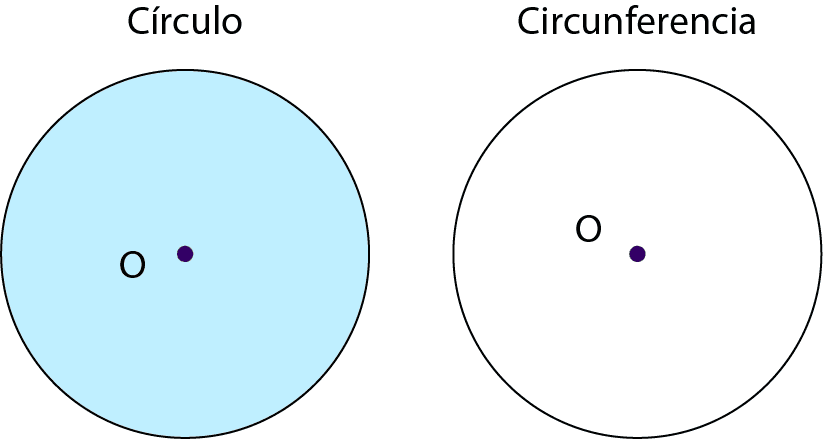
Un círculo es la región del plano delimitada por una circunferencia.
En cambio, una circunferencia es un conjunto infinito de puntos que se encuentran a la misma distancia de un punto fijo llamado centro (O).
1.2- Elementos de la Circunferencia
Los elementos de la circunferencia son:
a) Centro (O): Es un punto interior equidistante (que está a la misma distancia) de todos los puntos de la circunferencia.
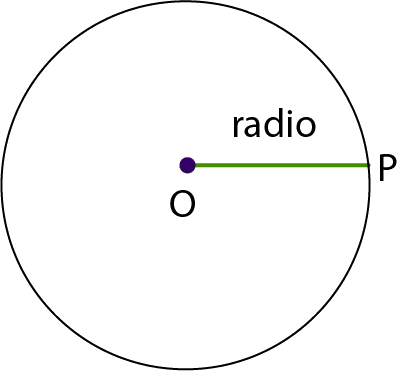
b) Radio: Es un segmento que une el centro (O) de la circunferencia con un punto cualquiera de ella. Todos los radios tienen igual medida y se denota con la letra r.
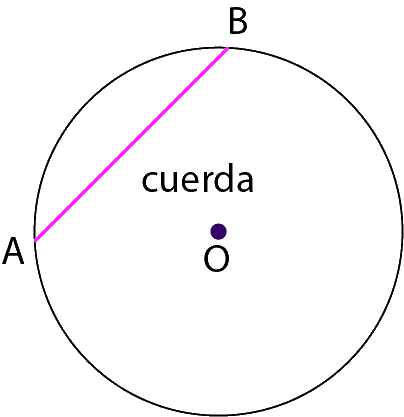
c) Cuerda: Representa al segmento que une dos puntos de la circunferencia. La cuerda entre A y B se denota
d) Diámetro: Es un segmento que une dos puntos de la circunferencia y que pasa por el centro (O), El diámetro también es conocido como cuerda mayor. Se denota por la letra d.

e) Arco: Es un segmento curvo de puntos que pertenecen a la circunferencia. Un arco entre los puntos A y B de una circunferencia se representa . Los arcos de una circunferencia se leen en sentido contrario de los punteros del reloj. En la figura, se marco con azul el arco y en amarillo el arco .

Medición de arcos:
Una forma de medir un arco es utilizando grados sexagesimales. La suma de las medidas de todos los arcos resulta 360°, es decir, el arco de la circunferencia completa mide 360°
g) Recta tangente: Es una recta que intersecta a la circunferencia en un punto único. Dicho punto se llama punto de tangencia.

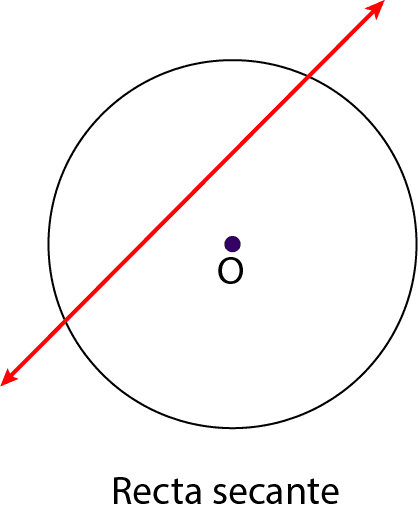
g) Recta secante: Es una recta que intersecta en exactamente dos puntos a la circunferencia.
Nota:
Debemos recordar que el diámetro es el doble del radio en una circunferencia, esto es:
Diámetro es el doble del radio es equivalente a decir que el radio es la mitad del diámetro.
Ahora vamos a estudiar dos de los ángulos que se forman en una circunferencia.
2- Ángulos en la circunferencia
2.1- Ángulo del centro en una circunferencia
Como podemos ver en este caso, el vértice del Ángulo está en el origen (O) de la circunferencia y sus lados son los radios de esta.
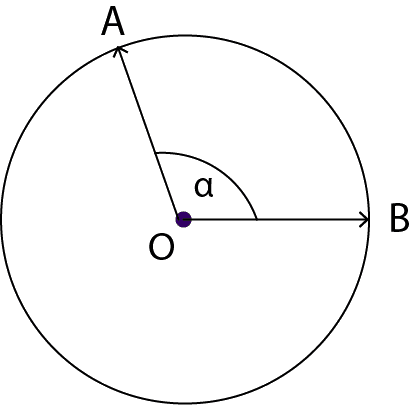
En este caso la medida del
àngulo del centro.
Ejemplos:
2.1.1- En la siguiente figura, ¿Cuál es la medida del arco ? sabiendo que el mide 115°?
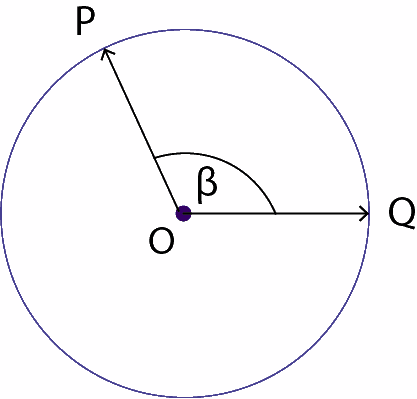
Respuesta: Como vimos anteriormente, la medida del ángulo que subtiende un determinado arco es igual a la medida del arco, luego °
2.1.2- ¿Cuál(es) de las siguiente(s) opción(es) es falsa?
A. En circunferencias congruentes los radios son congruentes.
B. La medida del diámetro de una circunferencia es el doble que la medida de su radio.
C. Por tres puntos cualesquiera siempre pasa una circunferencia.
D. La mayor cuerda de una circunferencia es el diámetro.
E. Al cortarse dos cuerdas en el centro de la circunferencia forman 4 ángulos del centro.
Respuesta:
Letra A: Es verdadera ya que, si dos circunferencias son congruentes, o sea, tienen la misma medida, luego sus radios también miden lo mismo.
Letra B: Es verdadera por definición de diámetro.
Letra C: Es Falsa, ya que si tengo tres puntos colineales B y D que no están a la misma distancia de C, nunca pasará una circunferencia por esos dos puntos.
Letra D: Es verdadera ya que la cuerda mayor, pasa por dos puntos de la circunferencia y el centro (O).
Letra E: Es verdadera ya que, siendo O el centro:

Tenemos entonces los ángulos del centro: .
2.1.3- Si se sabe que el arco mide la cuarta parte del total de la circunferencia, ¿Cuánto mide el ángulo que subtiende ese arco?
Respuesta: Como sabemos, la circunferencia corresponde a un ángulo completo, esto es, que mide 360°, luego si el arco es la cuarta parte de ella, el ángulo que subtiende dicho arco corresponde a un ángulo recto (90°)
2.2- Ángulo inscrito en una circunferencia
Aquí el origen del ángulo se encuentra en un punto de la circunferencia y sus lados son 2 rectas secantes a ella.
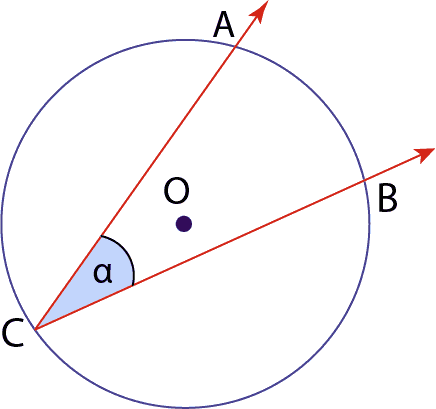
2.3- Teoremas del ángulo inscrito en una circunferencia
I. “Todo ángulo inscrito en una circunferencia mide la mitad del ángulo del centro que subtiende el mismo arco”.
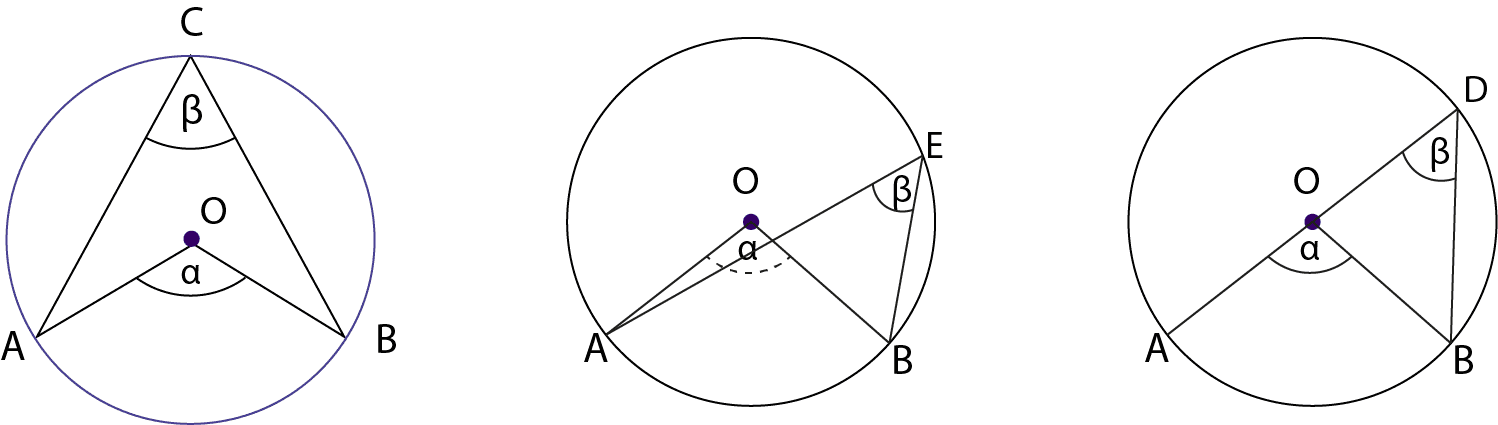
Donde O es el centro de la circunferencia.
ángulo del centro
ángulo inscrito
: arco que subtiende
Se tiene que:
II. “Todo ángulo inscrito en una semicircunferencia es recto, o sea, mide 90°”.
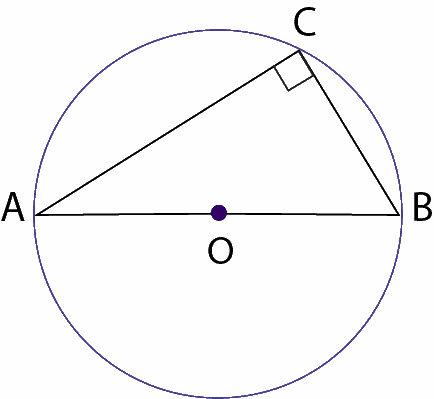
Donde: O es el centro de la circunferencia; diámetro de la circunferencia; y cuerdas de la circunferencia; inscrito en la circunferencia.
Ejemplo:
Se tiene una circunferencia de diámetro 5 cm, cuerda de 4 cm y otra de 3 cm.
Demostrar que él
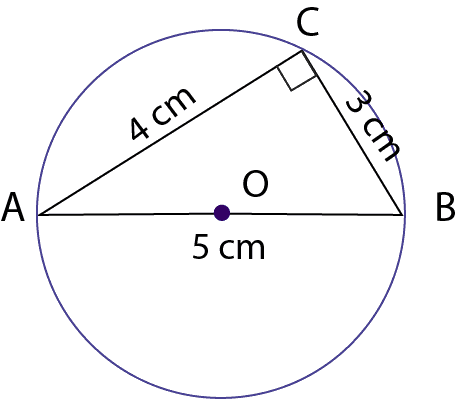
Para demostrar este teorema recordaremos el teorema de Pitágoras. El ángulo inscrito en el punto C debiera valer 90°, para esto veremos si se cumple el teorema de Pitágoras, esto es:
Comprobemos: deberìa ser igual a
Luego, como se cumple el teorema de Pitágoras, podemos concluir que
III. “Todos los ángulos inscritos en una circunferencia que subtienden un mismo arco tienen igual medida”.

Aquí:
Ejemplo:
En la circunferencia de centro O de la figura, se tiene que , entonces el valor del ángulo es:
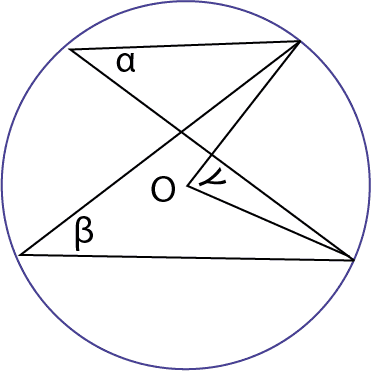
En este caso es un ángulo del centro, luego por el teorema visto anteriormente mide el doble de y por ser ángulos inscritos en la misma circunferencia y que subtienden el mismo arco que , tienen entre ellos la misma medida, o sea,
Como sabemos:
Por teorema I, del ángulo inscrito, podemos concluir que:

